Mêmes résultats avec python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1:37a07cee5969, Dec  5 2015, 21:12:44) 
[GCC 4.2.1 (Apple Inc. build 5666) (dot 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1

Cela se produit uniquement avec la distance euclidienne et peut être reproduit en utilisant directement sklearn.metrics.pairwise.euclidean_distances :

import scipy
import sklearn.metrics.pairwise

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)

# compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_32], [b_32])

np.set_printoptions(precision=200)

print(dist_64_sklearn)
print(dist_32_sklearn)

Je n'ai pas pu localiser davantage l'erreur.
J'espère que cela peut aider.

numpy peut utiliser un accumulateur de plus haute précision. oui, ça ressemble à ça
mérite d'être réparé.

Le 19 juillet 2017 à 00h05, "nvauquie" [email protected] a écrit:

Mêmes résultats avec python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1: 37a07cee5969, 5 décembre 2015, 21:12:44)
[GCC 4.2.1 (Apple Inc. build 5666) (point 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1

Cela se produit uniquement avec la distance euclidienne et peut être reproduit en utilisant
directement sklearn.metrics.pairwise.euclidean_distances:

importer scipy
import sklearn.metrics.pairwise

créer des vecteurs 64 bits a et b très similaires les uns aux autres

a_64 = np.array ([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype = np.float64)
b_64 = np.array ([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype = np.float64)

créer des versions 32 bits de a et b

a_32 = a_64.astype (np.float32)
b_32 = b_64.astype (np.float32)

calculer la distance de a à b en utilisant sklearn, à la fois pour 64 bits et 32 ​​bits

dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_32], [b_32])

np.set_printoptions (précision = 200)

imprimer (dist_64_sklearn)
imprimer (dist_32_sklearn)

Je n'ai pas pu localiser davantage l'erreur.
J'espère que cela peut aider.

-
Vous recevez ceci parce que vous êtes abonné à ce fil.
Répondez directement à cet e-mail, affichez-le sur GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-316074315 ,
ou couper le fil
https://github.com/notifications/unsubscribe-auth/AAEz65yy8Aq2FcsDAcWHT8qkkdXF_MfPks5sPLu_gaJpZM4OXbpZ
.

J'aimerais travailler là-dessus si possible

Fonce!

Je pense donc que le problème réside dans le fait que nous utilisons sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y)) pour calculer la distance euclidienne
Parce que si j'essaye - (-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) j'obtiens la réponse 0 pour np.float32, tandis que j'obtiens les bons ans pour np.float 64.

@jnothman Que pensez-vous que je devrais faire alors? Comme mentionné dans mon commentaire ci-dessus, le problème est probablement de calculer la distance euclidienne en utilisant sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

Vous dites donc que le point renvoie un résultat moins précis que le produit-puis-somme?

Non, ce que j'essaie de dire, c'est que dot renvoie un résultat plus précis que produit-puis-somme
-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) donne la sortie [[0.]]
tandis que np.sqrt(((X-Y) * (X-Y)).sum(axis=1)) donne la sortie [ 0.02290595]

Ce que vous faites n'est pas clair, en partie parce que vous ne publiez pas d'extrait de code entièrement autonome.

En regardant rapidement votre dernier message, les deux choses que vous essayez de comparer [[0.]] et [0.022...] n'ont pas les mêmes dimensions (peut-être un problème de copier-coller, mais encore une fois difficile à savoir parce que nous n'avons pas avoir un extrait complet).

Ok désolé mon mal

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
X = a_64.astype(np.float32)
Y = b_64.astype(np.float32)

X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]

#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
print(np.sqrt(distances))

#Euclidean distance computed using (X-Y)^2
print(np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis]))

PRODUCTION

[[ 0.03125]]
[[ 0.02290595136582851409912109375]]

La première méthode est de savoir comment elle est calculée par la fonction de distance euclidienne.
Aussi pour clarifier ce que je voulais dire ci-dessus, c'était le fait que la somme-alors-produit a une précision inférieure même lorsque nous utilisons des fonctions numpy pour le faire

Oui, je peux reproduire cela. Je vois que faire la soustraction au départ
permet de maintenir la précision de la différence. Faire le point
produit puis soustraire (ou annuler et ajouter), comme nous le faisons actuellement,
perd cette précision car les chiffres les plus significatifs sont bien plus grands que
les différences.

L'implémentation actuelle est plus efficace en mémoire pour un nombre élevé de
fonctionnalités. Mais je suppose que la distance euclidienne devient de moins en moins pertinente
en grandes dimensions, la mémoire est donc dominée par le nombre de sorties
valeurs.

Je vote donc pour l'adoption de la mise en œuvre la plus stable numériquement sur le
d-implémentation asymptotiquement efficace que nous avons actuellement. Un avis,
@ogrisel? @agramfort?

Et c'est bien sûr plus préoccupant puisque nous avons récemment autorisé float32s
être plus courante parmi les estimateurs.

Donc, pour cet exemple, product-then-sum fonctionne parfaitement bien pour np.float64, donc une solution possible pourrait être de convertir l'entrée en float64 puis de calculer le résultat et de renvoyer le résultat converti en float32. Je suppose que ce serait plus efficace, mais je ne sais pas si cela fonctionnerait bien pour un autre exemple.

la conversion en float64 ne sera pas plus efficace dans l'utilisation de la mémoire que
soustraction.

Oh oui, vous êtes désolé à ce sujet, mais je pense qu'utiliser float64 et ensuite faire un produit puis une somme serait plus efficace en calcul sinon en mémoire.

Et la raison de l'utilisation du produit puis de la somme était d'avoir plus d'efficacité de calcul et non d'efficacité de mémoire.

bien sûr, mais je ne pense pas qu'il y ait de raison de supposer que c'est en fait
plus efficace en termes de calcul, sauf pour ne pas avoir à réaliser
tableau intermédiaire. En supposant que nous limitons la mémoire de travail absolue (par ex.
chunking), pourquoi prendre le produit scalaire, doubler et soustraire les normes
être beaucoup plus efficace que la soustraction et la quadrature?

Fournir des repères?

Ok donc j'ai créé un script python pour comparer le temps pris par soustraction-puis-quadrature et conversion en float64 puis produit-puis-somme et il s'avère que si nous choisissons un X et Y comme de très gros vecteurs, les 2 résultats sont très différents . Aussi @jnothman vous aviez raison, la soustraction-puis-la quadrature est plus rapide.
Voici le script que j'ai écrit, s'il y a un problème, faites-le moi savoir

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
from timeit import default_timer as timer

for i in range(9):
    X = np.random.rand(1,3 * (10**i)).astype(np.float32)
    Y = np.random.rand(1,3 * (10**i)).astype(np.float32)

    X, Y = check_pairwise_arrays(X, Y)
    XX = row_norms(X, squared=True)[:, np.newaxis]
    YY = row_norms(Y, squared=True)[np.newaxis, :]

    #Euclidean distance computed using product-then-sum
    distances = safe_sparse_dot(X, Y.T, dense_output=True)
    distances *= -2
    distances += XX
    distances += YY

    ans1 = np.sqrt(distances)

    start = timer()
    ans2 = np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis])
    end = timer()
    if ans1 != ans2:
        print(end-start)

        start = timer()
        X = X.astype(np.float64)
        Y = Y.astype(np.float64)
        X, Y = check_pairwise_arrays(X, Y)
        XX = row_norms(X, squared=True)[:, np.newaxis]
        YY = row_norms(Y, squared=True)[np.newaxis, :]
        distances = safe_sparse_dot(X, Y.T, dense_output=True)
        distances *= -2
        distances += XX
        distances += YY
        distances = np.sqrt(distances)
        end = timer()
        print(end-start)
        print('')
        if abs(ans2 - distances) > 1e-3:
            # np.set_printoptions(precision=200)
            print(ans2)
            print(np.sqrt(distances))

            print(X, Y)
            break

il vaut la peine de tester sa mise à l'échelle avec le nombre d'échantillons, pas seulement
nombre de fonctionnalités ... prendre des normes peut avoir l'avantage de calculer certaines
choses une fois par échantillon, pas une fois par paire d'échantillons

Le 20 octobre 2017 à 02h39, "Osaid Rehman Nasir" [email protected]
a écrit:

Ok donc j'ai créé un script python pour comparer le temps pris par
soustraction-puis-quadrature et conversion en float64 puis produit-puis-somme
et il s'avère que si nous choisissons un X et Y comme très gros vecteurs, alors le 2
les résultats sont très différents. Aussi @jnothman https://github.com/jnothman
vous aviez raison, la soustraction, puis la quadrature est plus rapide.
Voici le script que j'ai écrit, s'il y a un problème, faites-le moi savoir

importer numpy comme np
importer scipy
à partir de sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
depuis sklearn.utils.extmath import safe_sparse_dot
à partir de timeit importez default_timer comme minuterie

pour i dans la plage (9):
X = np.random.rand (1,3 * (10 i)). Astype (np.float32)Y = np.random.rand (1,3 * (10 i)). Astype (np.float32)

X, Y = check_pairwise_arrays (X, Y)
XX = row_norms (X, squared = True) [:, np.newaxis]
YY = row_norms (Y, squared = True) [np.newaxis,:]

# Distance euclidienne calculée à l'aide du produit-puis-somme
distances = safe_sparse_dot (X, YT, dense_output = True)
distances * = -2
distances + = XX
distances + = YY

ans1 = np.sqrt (distances)

start = timer ()
ans2 = np.sqrt (row_norms (XY, squared = True) [:, np.newaxis])
end = minuterie ()
si ans1! = ans2:
impression (fin-début)

  start = timer()
  X = X.astype(np.float64)
  Y = Y.astype(np.float64)
  X, Y = check_pairwise_arrays(X, Y)
  XX = row_norms(X, squared=True)[:, np.newaxis]
  YY = row_norms(Y, squared=True)[np.newaxis, :]
  distances = safe_sparse_dot(X, Y.T, dense_output=True)
  distances *= -2
  distances += XX
  distances += YY
  distances = np.sqrt(distances)
  end = timer()
  print(end-start)
  print('')
  if abs(ans2 - distances) > 1e-3:
      # np.set_printoptions(precision=200)
      print(ans2)
      print(np.sqrt(distances))

      print(X, Y)
      break

-
Vous recevez cela parce que vous avez été mentionné.
Répondez directement à cet e-mail, affichez-le sur GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-337948154 ,
ou couper le fil
https://github.com/notifications/unsubscribe-auth/AAEz6z5o2Ao_7V5-Lflb4HosMrHCeOrVks5st209gaJpZM4OXbpZ
.

de toute façon, souhaitez-vous soumettre un PR, @ragnerok?

ouais bien sûr, que veux-tu que je fasse?

fournir une implémentation plus stable, également un test qui échouerait sous le
mise en œuvre actuelle, et idéalement un benchmark qui montre que nous ne perdons pas
beaucoup du changement, dans des cas raisonnables.

Je voulais demander s'il est possible de trouver la distance entre chaque paire de lignes avec vectorisation. Je ne peux pas penser à comment le faire vectorisé.

Vous voulez dire la différence (pas la distance) entre les paires de lignes? Bien sûr, vous pouvez le faire si vous travaillez avec des tableaux numpy. Si vous avez des tableaux avec des formes (n_samples1, n_features) et (n_samples2, n_features), il vous suffit de le remodeler en (n_samples1, 1, n_features) et (1, n_samples2, n_features) et faire la soustraction:

>>> X = np.random.randint(10, size=(10, 5))
>>> Y = np.random.randint(10, size=(11, 5))
X.reshape(-1, 1, X.shape[1]) - Y.reshape(1, -1, X.shape[1])

Ouais merci qui a vraiment aidé 😄

Je voulais également demander si je fournissais une implémentation plus stable, je n'utiliserai pas X_norm_squared et Y_norm_squared. Alors, est-ce que je les supprime également des arguments ou dois-je avertir que cela ne sert à rien?

Je pense qu'ils seront obsolètes, mais nous devrons peut-être être certains que
il n'y a aucun cas où nous devrions conserver cette version.

nous allons être très prudents en changeant cela. c'est un
mise en œuvre de longue date. nous devons être sûrs de ne ralentir aucun
cas. nous pourrions avoir besoin de faire l'opération en morceaux pour éviter une mémoire élevée
usage (ce qui est peut-être rendu plus délicat par le fait que cela s'appelle
au sein des fonctions qui se segmentent pour minimiser le retrait de la mémoire de sortie
distances par paires).

J'aimerais vraiment entendre d'autres développeurs de base qui connaissent le calcul
coûts et précision numérique ... @ogrisel , @lesteve , @rth ...

Le 5 novembre 2017 à 5 h 27, "Osaid Rehman Nasir" [email protected]
a écrit:

Je voulais aussi demander si je fournis une implémentation plus stable, je ne serai pas
en utilisant X_norm_squared et Y_norm_squared. Alors dois-je les supprimer du
arguments aussi ou devrais-je avertir que cela ne sert à rien?

-
Vous recevez cela parce que vous avez été mentionné.
Répondez directement à cet e-mail, affichez-le sur GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-341919282 ,
ou couper le fil
https://github.com/notifications/unsubscribe-auth/AAEz63izdpQGDEuW32m8Aob6rrsvV6q-ks5szKyHgaJpZM4OXbpZ
.

mais il serait plus facile de discuter précisément si vous ouvrez un PR

Ok, je vais ouvrir un PR alors, avec une implémentation très basique de cette fonction

La question est de savoir ce qu'il faut faire à ce sujet pour la version 0.20. Pourrait-il y avoir des améliorations simples / temporaires (événement au prix par exemple de l'utilisation de la mémoire) qui pourraient être envisagées?

La solution et l'analyse proposées dans # 11271 sont certainement très précieuses, mais il faudra peut-être plus de discussion pour s'assurer que c'est la solution optimale. En particulier, je suis préoccupé par le fait que nous avons maintenant des discussions en attente sur la mémoire de travail globale optimale dans https://github.com/scikit-learn/scikit-learn/issues/11506 en fonction du type de processeur, etc. ajouterait encore un autre niveau de segmentation et la complexité de l'ensemble serait d'obtenir un peu de contrôle IMO. Mais peut-être que c'est juste moi, à la recherche d'un deuxième avis.

Que pensez-vous qu'il faudrait faire à propos de ce problème pour la version @jnothman @amueller @ogrisel ?

La stabilité l'emporte sur l'efficacité. Les problèmes de stabilité doivent être résolus même lorsque
l'efficacité a encore besoin d'être peaufinée.

Le but de working_memory était de faire des choses comme la silhouette avec un grand échantillon
les tailles fonctionnent. Cela a également amélioré l'efficacité, mais cela peut être modifié
ligne.

Je crois fermement que nous devrions essayer d'obtenir un correctif pour euclidean_distances avec
float32 po. Nous l'avons cassé en 0.19 en supposant que nous pourrions faire
euclidean_distances fonctionne sur 32 bits de manière naïve.

Je suis d'accord que nous avons besoin d'une solution. Ma préoccupation ici n'est pas l'efficacité mais la complexité supplémentaire de la base de code.

En prenant du recul, l'implémentation euclidienne de scipy semble être 10 lignes de code C et pour 32 bits, il suffit de les convertir en 64 bits. Je comprends que ce n'est pas le plus rapide, mais il est conceptuellement facile à suivre et à comprendre. Dans scikit-learn, nous utilisons l'astuce pour accélérer les calculs dans BLAS, puis il y a des améliorations possibles dues à https://github.com/scikit-learn/scikit-learn/pull/10212 et maintenant la solution fragmentée possible à euclidean distance en 32 bits.

Je cherche juste des informations sur ce que devrait être la direction générale sur ce sujet (par exemple, essayez d'en remonter une partie pour scipy, etc.).

scipy ne semble pas concerné par la copie des données ...

Passez à 0,21 après le PR.

Supprimer le bloqueur?

sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

est numériquement instable, si le point (x, x) et le point (y, y) sont d'une magnitude similaire à celle du point (x, y) à cause de ce que l'on appelle l' annulation catastrophique .

Cela affecte non seulement la précision FP32, mais il est bien sûr plus important et échouera beaucoup plus tôt.

Voici un cas de test simple qui montre à quel point c'est mauvais, même avec une double précision:

import numpy
from sklearn.metrics.pairwise import euclidean_distances

a = numpy.array([[100000001, 100000000]])
b = numpy.array([[100000000, 100000001]])

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

a = numpy.array([[10001, 10000]], numpy.float32)
b = numpy.array([[10000, 10001]], numpy.float32)

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

sklearn calcule ici une distance de 0 les deux fois, plutôt que sqrt (2).

Une discussion des problèmes numériques de la variance et de la covariance - et cela se reporte trivialement à cette approche d'accélération de la distance euclidienne - peut être trouvée ici:

Erich Schubert et Michael Gertz.
Calcul parallèle numériquement stable de la (co-) variance.
In: Actes de la 30e Conférence internationale sur la gestion des bases de données scientifiques et statistiques (SSDBM), Bolzano-Bozen, Italie. 2018, 10: 1–10: 12

En fait, la coordonnée y peut être supprimée de ce cas de test, la distance correcte devient alors trivialement 1. J'ai fait une demande de tirage qui déclenche ce problème numérique:

    XA = np.array([[10000]], np.float32)
    XB = np.array([[10001]], np.float32)
    assert_equal(euclidean_distances(XA, XB)[0,0], 1)

Je ne pense pas que mon article mentionné ci-dessus fournisse une solution à ce problème - calculez simplement la distance euclidienne comme sqrt (sum (power ())) et il est en un seul passage et a une précision raisonnable. La perte est d'utiliser déjà les carrés, c'est-à-dire que le point (x, x) lui-même perd déjà la précision.

@amueller car le problème peut être plus grave que prévu, je suggère de rajouter le libellé du bloqueur ...

Merci pour cet exemple très simple.

La raison pour laquelle il est mis en œuvre de cette façon est parce que c'est beaucoup plus rapide. Voir ci-dessous:

x = np.random.random_sample((1000, 1000))

%timeit euclidean_distances(x,x)
20.6 ms ± 452 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit cdist(x,x)
695 ms ± 4.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Bien que le nombre d'opérations soit du même ordre dans les deux méthodes (1,5 fois plus dans la seconde), l'accélération vient de la possibilité d'utiliser des bibliothèques BLAS bien optimisées pour la multiplication matricielle matricielle.

Ce serait un énorme ralentissement pour plusieurs estimateurs dans scikit-learn.

Oui, mais seulement 3-4 chiffres de précision avec FP32 et 7-8 chiffres avec FP64 ne cause importante imprécision, non? En particulier, puisque ces erreurs ont tendance à s'amplifier ...

Eh bien, je ne dis pas que tout va bien pour le moment. :)
Je dis que nous devons trouver une solution entre les deux.
Il y a un PR (# 11271) qui propose de lancer sur float64 pour faire les calculs. In ne résout pas le problème pour float64 mais donne une meilleure précision pour float32.

Avez-vous un exemple où l'utilisation d'un estimateur qui utilise euclidean_distances donne des résultats erronés en raison de la perte de précision?

Je pense toujours que c'est un gros problème et que cela devrait être un bloqueur pour 0,21. C'était un problème introduit pour 32 bits dans la version 0.19, et ce n'est pas un bon état de choses à quitter. J'aurais aimé que nous l'ayons résolu plus tôt en 0.20, et je serais d'accord, ou même désireux, de voir # 11271 fusionné dans l'intervalle. Les seuls problèmes dans ce PR que je connaisse de l'optimisation surround de l'efficacité de la mémoire, qui est un trou de lapin profond.

Nous avons cette version "rapide" depuis longtemps, mais toujours en float64. Je sais, @ kno10 , qu'il y a des problèmes de précision. Avez-vous une bonne heuristique rapide pour nous de déterminer quand cela pourrait être un problème et utiliser une solution plus lente mais plus sûre?

Oui, mais seulement 3-4 chiffres de précision avec FP32 et 7-8 chiffres avec FP64 provoquent une imprécision substantielle, n'est-ce pas

Merci d'avoir illustré ce problème avec un exemple très simple!

Cependant, je ne pense pas que le problème soit aussi répandu que vous le suggérez - il affecte principalement les échantillons dont la distance mutuelle est petite par rapport à leurs normes.

La figure ci-dessous illustre cela, pour 2e6 paires d'échantillons aléatoires, où chaque échantillon 1D est dans l'intervalle [-100, 100]. L'erreur relative entre l'implémentation scikit-learn et scipy est tracée en fonction de la distance entre les échantillons, normalisée par leurs normes L2, c'est-à-dire,

d_norm(A, B) = d(A, B) / sqrt(‖A‖₂*‖B‖₂)

(pas sûr que ce soit le bon paramétrage, mais juste pour obtenir des résultats quelque peu invariants à l'échelle des données),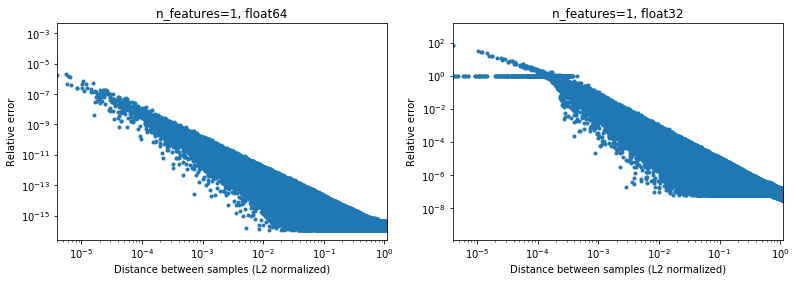

Par exemple,

1. si l'on prend [10000] et [10001] la distance normalisée L2 est 1e-4 et l'erreur relative sur le calcul de la distance sera 1e-8 en 64 bits, et> 1 en 32 bits (Ou 1e -8 et> 1 en valeur absolue respectivement). En 32 bits, ce cas est en effet assez terrible.
2. par contre pour [1] et [10001] , l'erreur relative sera ~ 1e-7 en 32 bits, ou la précision maximale possible.

La question est de savoir à quelle fréquence 1. le cas se produira dans la pratique dans les applications de ML.

Fait intéressant, si l'on passe à la 2D, toujours avec une distribution aléatoire uniforme, il sera difficile de trouver des points très proches,

Bien sûr, en réalité, nos données ne seront pas échantillonnées uniformément, mais pour toute distribution en raison de la malédiction de la dimensionnalité, la distance entre deux points quelconques convergera lentement vers des valeurs très similaires (différentes de 0) à mesure que la dimensionnalité augmente. Bien qu'il s'agisse d'un problème général de ML, il peut ici atténuer quelque peu ce problème de précision, même pour une dimensionnalité relativement faible. Ci-dessous les résultats pour n_features=5 ,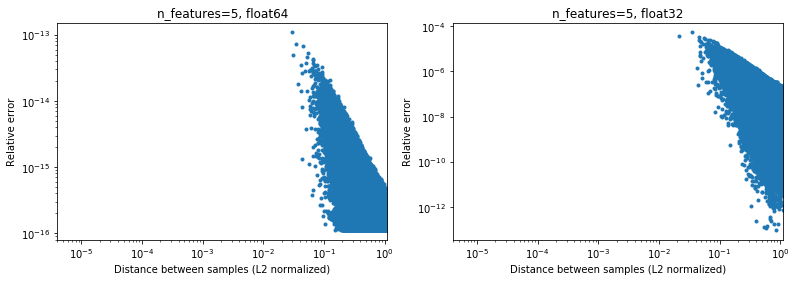
.

Donc, pour les données centrées, au moins en 64 bits, ce n'est peut-être pas tellement un problème en pratique (en supposant qu'il y ait plus de 2 fonctionnalités). La vitesse de calcul 50x (comme illustré ci-dessus) peut en valoir la peine (en 64 bits). Bien sûr, on peut toujours ajouter 1e6 à certaines données normalisées en [-1, 1] et dire que les résultats ne sont pas précis, mais je dirais que la même chose s'applique à un certain nombre d'algorithmes numériques, et en travaillant avec des données exprimées dans le 6ème chiffre significatif est juste à la recherche de problèmes.

(Le code des chiffres ci-dessus se trouve ici ).

Toute approche rapide utilisant la version point (x, x) + point (y, y) -2 point (x, y) aura probablement le même problème pour tout ce que je peux dire, mais vous feriez mieux de demander à un vrai expert en numérique pour ça. la précision des données d'

Je ne peux pas dire combien de frais généraux vous obtenez en convertissant float32 en float64 à la volée pour utiliser cette approche. Au moins pour float32, à ma connaissance, faire tous les calculs et stocker les produits scalaires comme float64 devrait être bien.

À mon humble avis, les gains de performance (qui ne sont pas exponentiels, juste un facteur constant) ne valent pas la perte de précision (qui peut vous mordre de manière inattendue) et la bonne façon est de ne pas utiliser cette astuce problématique. Il peut cependant être tout à fait possible d'optimiser davantage le code en effectuant le calcul "traditionnel", par exemple pour utiliser AVX. Parce que sum ((xy) * 2) est presque difficile à implémenter dans AVX.Au minimum, je suggérerais de renommer la méthode en approximate_euclidean_distances , en raison de la précision parfois faible (ce qui empire plus les deux valeurs sont proches, ce qui * peut être bien au départ, puis commence à avoir de l'importance lors de la convergence vers un optimum) , afin que les utilisateurs soient conscients de ce problème.

@rth merci pour les illustrations. Mais que faire si vous essayez d'optimiser, par exemple, x vers un optimum. Très probablement, l'optimum ne sera pas à zéro (s'il s'agissait toujours de votre centre de données, la vie serait excellente), et finalement les deltas que vous calculez pour les gradients, etc. peuvent avoir de très petites différences.
De même, en clustering, les clusters n'auront pas tous leurs centres proches de zéro, mais en particulier avec de nombreux clusters, x ≈ centre avec quelques chiffres est tout à fait possible.

Dans l'ensemble cependant, je suis d'accord que ce problème doit être résolu. Dans tous les cas, nous devons documenter les problèmes de précision de l'implémentation actuelle dès que possible.

En général, je ne pense pas que cette discussion devrait avoir lieu dans scikit-learn. La distance euclidienne est utilisée dans divers domaines de l'informatique scientifique et la liste de diffusion scipy de l'OMI est un meilleur endroit pour en discuter: cette communauté a également plus d'expérience avec ces problèmes de précision numérique. En fait, nous avons ici un algorithme rapide mais quelque peu approximatif. Il se peut que nous devions implémenter des solutions de contournement à court terme, mais à long terme, il serait bon de savoir que cela y sera apporté.

Pour 32 bits, https://github.com/scikit-learn/scikit-learn/pull/11271 peut en effet être une solution, je ne suis tout simplement pas aussi désireux de plusieurs niveaux de segmentation tout au long de la bibliothèque car cela augmente la complexité du code et que vous voulez vous assurer qu'il n'y a pas de meilleur moyen de contourner ce problème.

Merci pour votre réponse @ kno10! (Mes commentaires ci-dessus n'en tiennent pas encore compte) Je vous répondrai un peu plus tard.

Oui, la convergence vers un point en dehors de l'origine peut être un problème.

À mon humble avis, les gains de performance (qui ne sont pas exponentiels, juste un facteur constant) ne valent pas la perte de précision (qui peut vous mordre de manière inattendue) et la bonne façon est de ne pas utiliser cette astuce problématique.

Eh bien, un ralentissement> 10x de leur calcul en 64 bits aura un effet très réel sur les utilisateurs.

Il peut cependant être tout à fait possible d'optimiser davantage le code en effectuant le calcul "traditionnel", par exemple pour utiliser AVX. Parce que sum ((xy) ** 2) est presque difficile à implémenter dans AVX.

J'ai essayé une implémentation naïve rapide avec numba (qui devrait utiliser SSE),

@numba.jit(nopython=True, fastmath=True)              
def pairwise_distance_naive(A, B):
    n_samples_a, n_features_a = A.shape
    n_samples_b, n_features_b = B.shape
    assert n_features_a == n_features_b
    distance = np.empty((n_samples_a, n_samples_b), dtype=A.dtype)
    for i in range(n_samples_a):
        for j in range(n_samples_b):
            psum = 0.0
            for k in range(n_features_a):
                psum += (A[i, k] - B[j, k])**2
            distance[i, j] = math.sqrt(psum)
    return distance

obtenir une vitesse similaire à scipy cdist jusqu'à présent (mais je ne suis pas un expert en numba), et également pas sûr de l'effet de fastmath .

en utilisant la version point (x, x) + point (y, y) -2 * point (x, y)

Juste pour référence future, ce que nous faisons actuellement est à peu près le suivant (car il y a une dimension qui ne s'affiche pas dans la notation ci-dessus),

def quadratic_pairwise_distance(A, B):
    A2 = np.einsum('ij,ij->i', A, A)
    B2 = np.einsum('ij,ij->i', B, B)
    return np.sqrt(A2[:, None] + B2[None, :] - 2*np.dot(A, B.T))

où einsum et dot utilisent maintenant BLAS. Je me demande, si en plus d'utiliser BLAS, cela fait également le même nombre d'opérations mathématiques que la première version ci-dessus.

Je me demande, si en plus d'utiliser BLAS, cela fait également le même nombre d'opérations mathématiques que la première version ci-dessus.

Non. Le ((x - y) * 2.sum ()) effectue* n_samples_x * n_samples_y * n_features * (1 soustraction + 1 addition + 1 multiplication)
alors que xx + yy -2x.y effectue
n_samples_x * n_samples_y * n_features * (1 addition + 1 multiplication) .
Il y a un ratio 2/3 pour le nombre d'opérations entre les 2 versions.

Suite à la discussion ci-dessus,

• Création d'un PR pour permettre éventuellement de calculer les distances euclidiennes exactement https://github.com/scikit-learn/scikit-learn/pull/12136
• Quelques WIP pour voir si nous pouvons détecter et atténuer les points problématiques dans https://github.com/scikit-learn/scikit-learn/pull/12142

Pour 32 bits, nous devons toujours fusionner https://github.com/scikit-learn/scikit-learn/pull/11271 sous une forme ou une autre si l'OMI, les PR ci-dessus sont quelque peu orthogonales.

FYI: lors de la résolution de certains problèmes dans OPTICS et de l'actualisation du test pour utiliser les résultats de référence d'ELKI, ceux-ci échouent avec metric="euclidean" mais réussissent avec metric="minkowski" . Les différences numériques sont suffisamment importantes pour provoquer un ordre de traitement différent (il ne suffit pas de diminuer le seuil).

https://github.com/kno10/scikit-learn/blob/ab544709a392e4dc7b22e9fd60c4755baf3d3053/sklearn/cluster/tests/test_optics.py#L588

Je ne suis vraiment pas au courant, mais je suis surpris qu'il n'y ait pas de solution existante. Cela semble être un calcul très courant et il semble que nous réinventons la roue. Quelqu'un a-t-il essayé de toucher la communauté informatique scientifique au sens large?

Pas encore, mais je suis d'accord que nous devrions. La seule chose que j'ai trouvée à ce sujet dans scipy était https://github.com/scipy/scipy/pull/2815 et les problèmes liés.

Je pense que @jeremiedbb pourrait avoir une idée?

Malheureusement pas encore satisfaisant :(

Nous aimerions nous appuyer sur une bibliothèque hautement optimisée pour ce type de calcul, comme nous le faisons pour l'algèbre linéaire avec des bibliothèques BLAS telles que OpenBLAS ou MKL. Mais la distance euclidienne n'en fait pas partie. L'astuce par points est une tentative de faire cela en s'appuyant sur le sous-programme de multiplication matrice-matrice de niveau 3 BLAS. Mais ce n'est pas précis et il n'y a aucun moyen de le rendre plus précis en utilisant la même méthode. Nous devons abaisser nos attentes soit en termes de vitesse, soit en termes de précision.

Je pense que dans certaines situations, une précision totale n'est pas obligatoire et conserver la méthode rapide est très bien. C'est à ce moment que les distances sont utilisées pour les tâches «trouver les plus proches». Les problèmes de précision dans la méthode rapide apparaissent lorsque les distances entre les points sont faibles par rapport à leur norme (dans un rapport ~ <1e-4 pour float 32 et ~ <1e-8 pour float64). Tout d'abord, pour que cette situation se produise, l'ensemble de données doit être assez dense. Ensuite, pour avoir une erreur de commande, vous devez avoir les deux points les plus proches à peu près à la même distance. De plus, dans ce cas, d'un point de vue ML, les deux conduiraient à des ajustements presque aussi bons.

Dans la situation ci-dessus, nous pouvons faire quelque chose pour réduire la fréquence de ces mauvais ordres (jusqu'à 0?). Dans la situation d'argmin de distance par paire. Nous pouvons déplacer le désordre vers des points qui ne sont pas les plus proches. En utilisant essentiellement le fait que l'une des normes n'est pas nécessaire pour trouver l'argmin, voir le commentaire . Il a 2 avantages. C'est un plus robuste (jusqu'à présent je n'ai pas encore trouvé de mauvaise commande) et c'est encore plus rapide car cela évite certains calculs.

Un inconvénient, toujours dans la même situation, si à la fin on veut les distances réelles aux points les plus proches, les distances calculées avec la méthode ci-dessus ne peuvent pas être utilisées. Ils ne sont que partiellement calculés et ils ne sont de toute façon pas précis. Nous devons recalculer les distances de chaque point à son point le plus proche. Mais c'est rapide car pour chaque point il n'y a qu'une seule distance à calculer.

Je me demande que ce que j'ai décrit ci-dessus couvre tout le cas d'utilisation de euclidean_distances dans sklearn. Mais je suggère de le faire partout où cela peut être appliqué. Pour ce faire, nous pouvons ajouter un nouveau paramètre à euclidean_distances pour ne calculer que la partie nécessaire afin de l'enchaîner avec argmin. Ensuite, utilisez-le dans pairwise_distances_argmin et dans pairwise_distances_argmin_min (recalculer les distances minimales réelles à la fin de ce dernier).

Lorsque nous ne pouvons pas faire cela, revenez à celui qui est lent mais précis, ou ajoutez un commutateur comme dans # 12136.
Nous pouvons essayer de l'optimiser un peu pour réduire la baisse des performances car je conviens que cela ne semble pas optimal. J'ai quelques idées pour cela.

Une autre possibilité de continuer à utiliser BLAS est de combiner axpy avec nrm2 mais c'est loin d'être optimal. Les deux sont des fonctions BLAS de niveau 1, et il s'agit d'une copie. Ce ne serait que plus rapide en dimension> 100.
Idéalement, nous aimerions que la distance euclidienne soit incluse dans BLAS ...

Enfin, il existe une autre solution, consistant à upcasting. Ceci est fait dans # 11271 pour float32. L'avantage est que la vitesse n'est que la moitié de celle actuelle et que la précision est conservée. Cela ne résout cependant pas le problème de float64. Peut-être que nous pouvons trouver un moyen de faire une chose similaire dans cython pour float64. Je ne sais pas exactement comment mais en utilisant 2 nombres float64 pour simuler en quelque sorte un float128. Je peux essayer pour voir si c'est quelque peu faisable.

Idéalement, nous aimerions que la distance euclidienne soit incluse dans BLAS ...

Est-ce quelque chose que les bibliothèques envisageraient? Si OpenBLAS le faisait, nous serions déjà dans une assez bonne situation ...

Aussi, quelles sont les différences exactes entre nous le faisons et le BLAS le faisant? Détecter les capacités du processeur et décider quelle implémentation utiliser, ou quelque chose comme ça? Ou simplement avoir des versions compilées pour des architectures plus diverses?
Ou juste plus de temps / d'énergie à écrire des implémentations efficaces?

Ceci est intéressant: une implémentation alternative de la méthode fast instable mais prétendant être beaucoup plus rapide que sklearn:
https://github.com/droyed/eucl_dist
(ne résout pas du tout ce problème bien que lol)

Cette discussion semble liée https://github.com/scipy/scipy/issues/5657

Voici ce que fait Julia: https://github.com/JuliaStats/Distances.jl/blob/master/README.md#precision -for-euclidean-and-sqeuclidean
Il permet de définir un seuil de précision pour forcer le recalcul.

Répondre à ma propre question: OpenBLAS a ce qui ressemble à un assemblage manuscrit pour chaque processeur (pas l'architecture!) Et heutistics pour choisir des noyaux pour différentes tailles de problème. Donc, je ne pense pas que ce soit autant un problème de l'intégrer dans openblas que de trouver quelqu'un pour écrire / optimiser tous ces noyaux ...

Merci pour les pensées supplémentaires!

Dans une réponse partielle,

Nous aimerions nous appuyer sur une bibliothèque hautement optimisée pour ce type de calcul, comme nous le faisons pour l'algèbre linéaire avec des bibliothèques BLAS telles que OpenBLAS ou MKL.

Ouais, j'espérais aussi que nous pourrions en faire plus avec BLAS. La dernière fois, je n'ai rien cherché dans l'API BLAS standard (mais je ne suis pas un expert en la matière). BLIS pourrait offrir plus de flexibilité, mais comme nous ne l'utilisons pas par défaut, son utilisation est quelque peu limitée (bien que numpy puisse un jour https://github.com/numpy/numpy/issues/7372)

Voici ce que fait Julia: Il permet de définir un seuil de précision pour forcer le recalcul.

Bon de savoir!

Devrions-nous ouvrir un problème distinct pour le calcul approximatif plus rapide lié ci-dessus? Semble intéressant

Leur accélération sur le processeur de x2-x4 pourrait être due à https://github.com/scikit-learn/scikit-learn/pull/10212 .

Je préférerais ouvrir un problème sur scipy une fois que nous aurons suffisamment étudié cette question pour trouver une solution raisonnable (et éventuellement la rétroporter) car je pense que la distance euclidienne est quelque chose d'assez basique qui devrait intéresser de nombreuses personnes en dehors de ML (et en même temps, il serait utile d'avoir l'opinion des gens là-bas, par exemple sur les problèmes de précision).

C'est jusqu'à 60x, non?

Ceci est intéressant: une implémentation alternative de la méthode instable rapide mais prétendant être beaucoup plus rapide que sklearn

hum pas sûr à ce sujet. Ils comparent %timeit pairwise_distances(a,b, 'sqeuclidean') , qui utilise celui de scipy. Ils devraient faire %timeit pairwise_distances(a,b, 'euclidean', metric_params={'squared': True}) et leur accélération ne serait pas aussi bonne :)
Comme montré bien plus tôt dans la discussion, sklearn peut être 35 fois plus rapide que scipy

Oui, leurs benchmarks sont seulement 30% meilleurs avec metric="euclidean" (au lieu de squeclidean ),

In [1]: from eucl_dist.cpu_dist import dist                                                                                                                  
    ... import numpy as np                                                                                                                                   
In [4]: rng = np.random.RandomState(1)                                                                                                                        
    ... a = rng.rand(1000, 300)                                                                                                                              
    ...b = rng.rand(1000, 300)                                                                                                                              

In [7]: from sklearn.metrics.pairwise import pairwise_distances                                                                                              
In [8]: %timeit pairwise_distances(a, b, 'sqeuclidean')                                                                                                      
214 ms ± 2.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [9]: %timeit pairwise_distances(a, b)                                                                                                                     
27.4 ms ± 2.48 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [10]: from eucl_dist.cpu_dist import dist                                                                                                                 
In [11]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float32')                                                                                
20.8 ms ± 330 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [12]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float64')                                                                                
20.4 ms ± 222 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Est-ce quelque chose que les bibliothèques envisageraient? Si OpenBLAS le faisait, nous serions déjà dans une assez bonne situation ...

Cela ne semble pas simple. BLAS est un ensemble de spécifications pour les routines d'algèbre linéaire et il en existe plusieurs implémentations. Je ne sais pas à quel point ils sont ouverts à l'ajout de nouvelles fonctionnalités qui ne figurent pas dans les spécifications d'origine. Pour cela, peut-être que blis serait plus ouvert, mais comme dit précédemment, ce n'est pas la valeur par défaut pour le moment.

Ouvert https://github.com/scikit-learn/scikit-learn/issues/12600 sur le traitement sqeuclidean vs euclidean en pairwise_distances .

J'ai besoin de quelques éclaircissements sur ce que nous voulons pour cela. Voulons-nous que pairwise_distances soit proche - au sens de all_close - à la fois pour «euclidien» et «sqeuclidean»?

C'est un peu délicat. Parce que x est proche de y ne signifie pas que x² est proche de y². La précision est perdue lors de la mise au carré.

La solution de contournement de Julia liée ci-dessus est très intéressante et est assez simple à mettre en œuvre. Cependant, je soupçonne que cela ne fonctionne pas comme prévu pour «sqeuclidean». Je soupçonne que vous devez définir le seuil en dessous pour obtenir la précision souhaitée.

Le problème avec la définition d'un seuil très bas est que cela induit beaucoup de recalculs et une énorme baisse de performances. Cependant, cela est atténué par la dimension de l'ensemble de données. Le même seuil déclenchera beaucoup moins de recalculs en haute dimension (les distances sont plus grandes).

Peut-être pouvons-nous avoir 2 implémentations et basculer en fonction de la dimension de l'ensemble de données. Le plus lent mais sûr pour ceux de faible dimension (il n'y a pas beaucoup de différence entre scipy et sklearn dans ce cas de toute façon) et le fast + threshold pour ceux de haute dimension.

Cela nécessitera quelques repères pour trouver quand changer et définir le seuil, mais cela peut être une lueur d'espoir :)

Voici quelques points de repère pour la comparaison de vitesse entre scipy et sklearn. Les benchmarks comparent sklearn.metrics.pairwise.euclidean_distances(X,X) avec scipy.spatial.distance.cdist(X,X) pour les X de toutes tailles. Le nombre d'échantillons va de 2⁴ (16) à 2¹³ (8192), et le nombre de caractéristiques va de 2⁰ (1) à 2¹³ (8192).

La valeur dans chaque cellule est l'accélération de sklearn vs scipy, c'est-à-dire que moins de 1 sklearn est plus lent et au-dessus de 1 sklearn est plus rapide.

Le premier benchmark utilise l'implémentation MKL de BLAS et un seul cœur.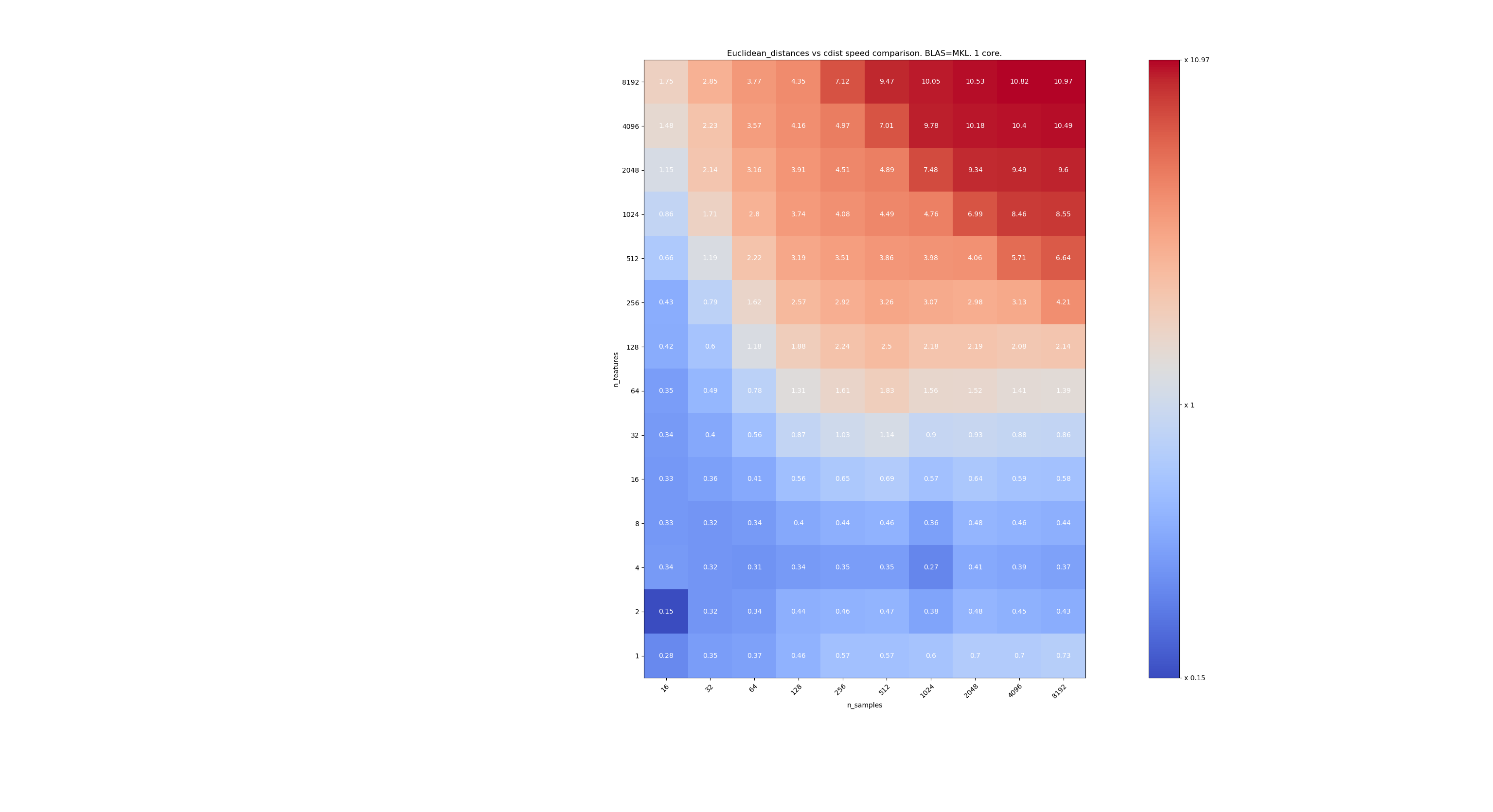

Le second utilise l'implémentation OpenBLAS de BLAS et un seul cœur. C'est juste pour vérifier que MKL et OpenBLAS ont le même comportement.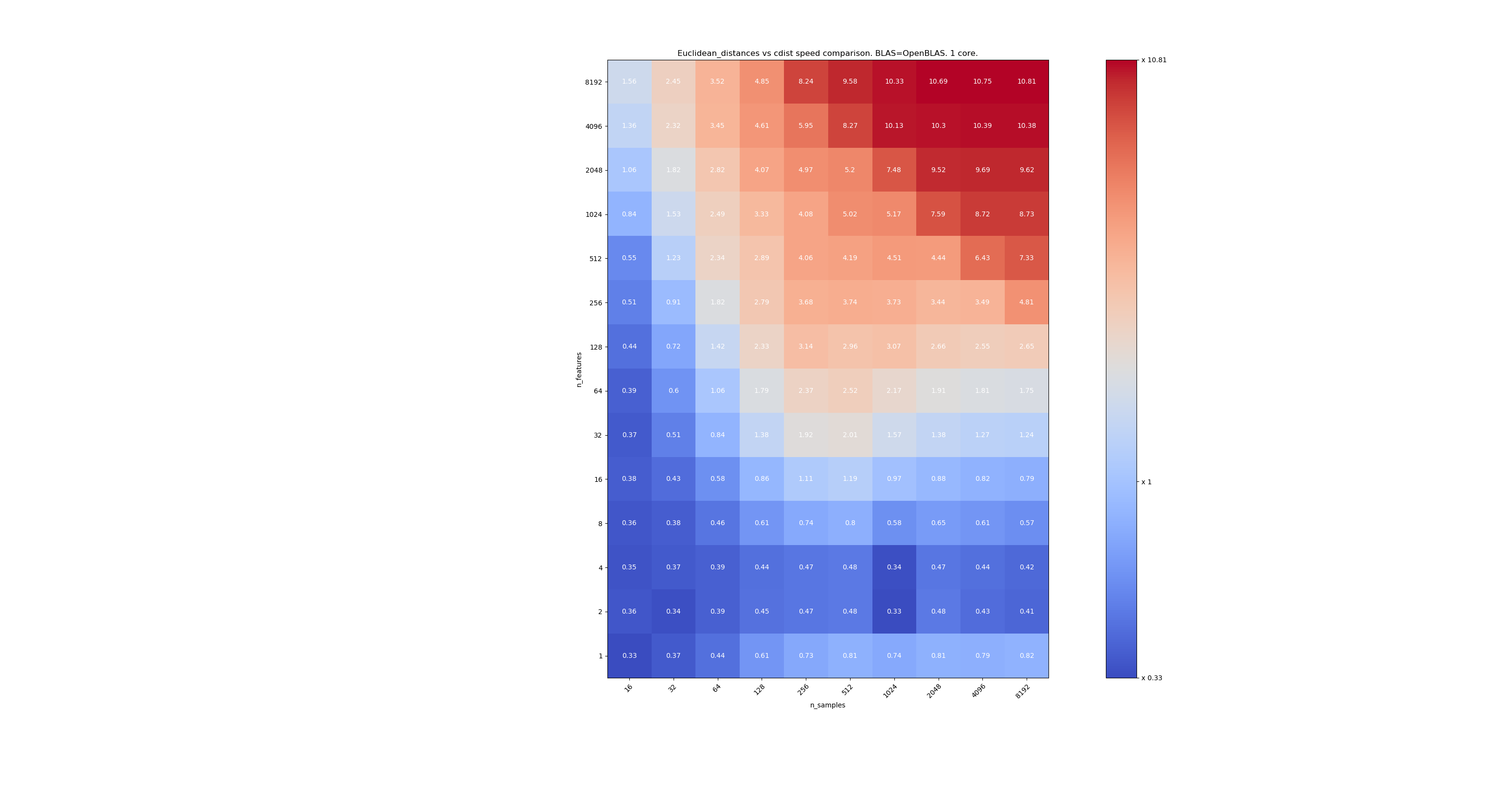

Le troisième utilise l'implémentation MKL de BLAS et 4 cœurs. Le fait est que euclidean_distances est parallélisé via une fonction BLAS LEVEL 3 mais cdist utilise uniquement une fonction BLAS LEVEL 1. Fait intéressant, cela ne change presque pas la frontière.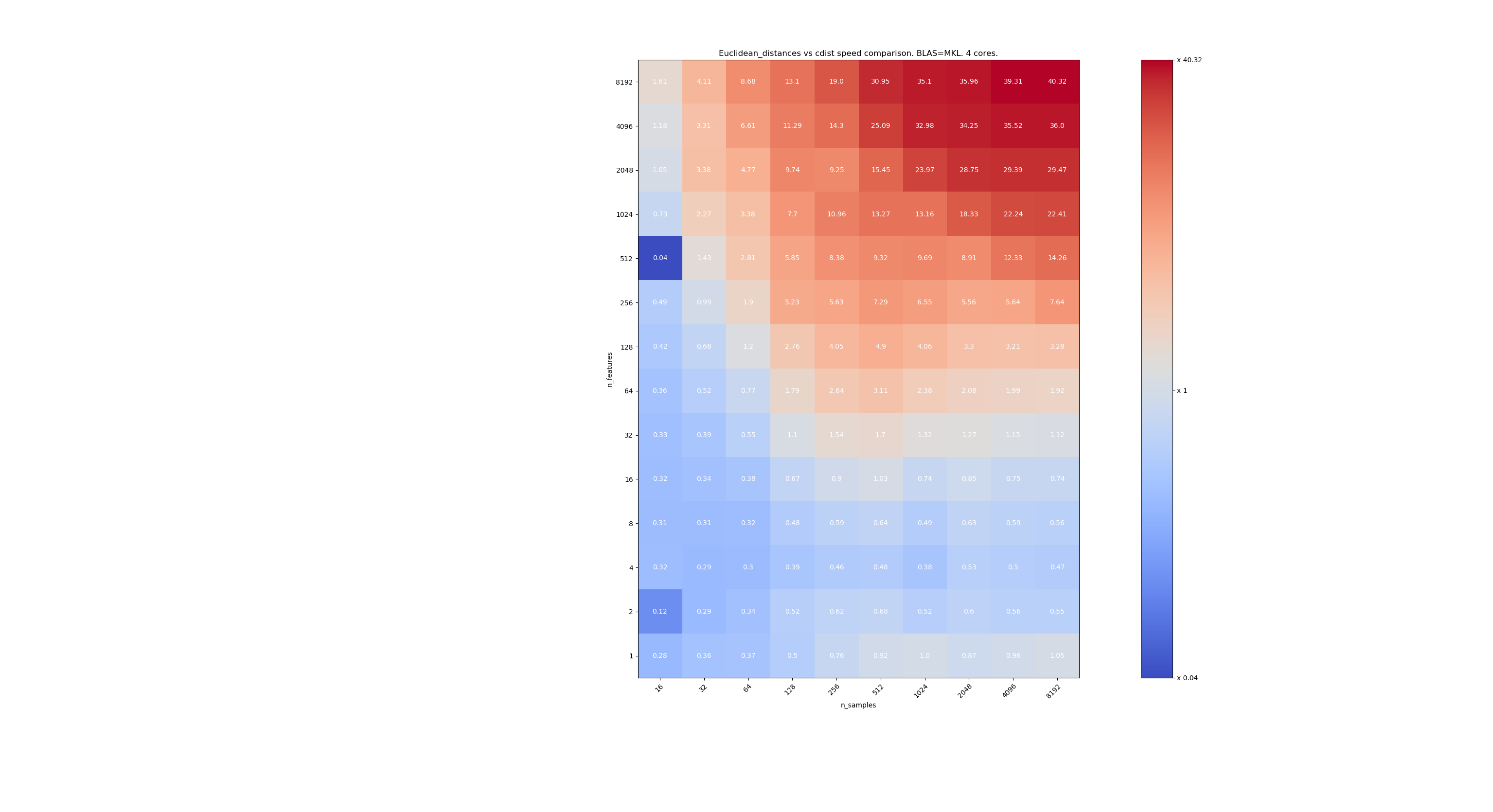

Lorsque n_samples n'est pas trop bas (> 100), il semble que la frontière se situe autour de 32 entités. Nous pourrions décider d'utiliser cdist quand n_features <32 et euclidean_distances quand n_features> 32. C'est plus rapide et il n'y a pas de problème de précision. Cela présente également l'avantage que lorsque n_features est petit, le seuil de julia conduit à de nombreux recalculs. L'utilisation de cdist évite cela.

Lorsque n_features> 32, nous pouvons garder l'implémentation euclidean_distances , mise à jour avec le seuil julia. L'ajout du seuil ne devrait pas trop ralentir euclidean_distances car le nombre de fonctionnalités est suffisamment élevé pour que seuls quelques recalculs soient nécessaires.

@jeremiedbb super, merci pour l'analyse. La conclusion me semble être un excellent moyen d’avancer.

Oh, je suppose que c'était tout pour float64, non? Que faisons-nous avec float32? upcast toujours? upcast pour> 32 fonctionnalités?

Je n'ai pas lu attentivement les commentaires (bientôt), juste pour info que float64 a ses limites, voir # 12128

@ qinhanmin2014 oui, la précision float64 a des limites, mais elle est suffisamment précise pour produire des résultats fp32 fiables pour tout ce que je peux dire. La question est de savoir à quels paramètres une conversion ascendante vers fp64 est réellement moins chère que l'utilisation de cdist de scipy.
Comme on le voit dans les benchmarks ci-dessus, même le BLAS multicœur n'est généralement pas plus rapide. Cela semble être principalement valable pour les données de haute dimension (plus de 64 dimensions; avant cela, l'avantage ne vaut généralement pas l'effort à mon humble avis) - et comme les distances euclidiennes ne sont pas aussi fiables dans les données denses de haute dimension, ce cas d'utilisation IMHO n'est pas de la plus haute importance . De nombreux utilisateurs auront moins de 10 dimensions. Dans ces cas, cdist semble généralement être plus rapide?

Oh, je suppose que c'était tout pour float64, non?

En fait, c'est pour float32 et float64 (je veux dire très similaire). Je suggère de toujours utiliser cdist lorsque n_features <32.

La question est de savoir à quels paramètres une conversion ascendante vers fp64 est réellement moins chère que l'utilisation de cdist de scipy.

L'upcasting ralentira d'un facteur ~ 2, donc je suppose que n_features = 64.

De nombreux utilisateurs auront moins de 10 dimensions.

Mais pas tout le monde, nous devons donc encore trouver une solution pour les données de grande dimension.

Très belle analyse @jeremiedbb !

Pour les données de faible dimension, il serait certainement judicieux d'utiliser cdist alors.

En outre, la cdist de scipy pour info transmet float32 à float64 https://github.com/scipy/scipy/issues/8771#issuecomment -384015674, je ne suis pas sûr si cela est dû à des problèmes de précision ou à autre chose.

Dans l'ensemble, je pense qu'il pourrait être judicieux d'ajouter le paramètre "algorithme" à euclidean_distance comme suggéré dans https://github.com/scikit-learn/scikit-learn/pull/12601#pullrequestreview -176076355, éventuellement avec une valeur par défaut sur "Aucun" afin qu'il puisse également être défini via une option globale comme dans https://github.com/scikit-learn/scikit-learn/pull/12136.

Il y a aussi une approche intéressante dans Eigen3 pour calculer des normes stables: https://eigen.tuxfamily.org/dox/StableNorm_8h_source.html (que je n'ai pas encore vraiment grokked)

Bonne explication, amélioré ma compréhension

Nous n'avons fait aucun progrès à ce sujet au sprint et nous devrions probablement ... et @rth n'est pas là aujourd'hui.

Je peux rejoindre à distance si vous définissez une heure. Peut-être en début d'après-midi?

Pour résumer la situation,

Pour les problèmes de précision dans les calculs de distance euclidienne,

• dans le cas de faible dimension, comme @jeremiedbb l'a montré ci-dessus, nous devrions probablement utiliser cdist
• dans le cas de haute dimension et float32, nous pourrions choisir entre,
  
  
  
  • segmentation, calcul de la distance en 64 bits et concaténation
  
  
  • revenir à cdist dans les cas où la précision est un problème (comment une question ouverte - tendre la main par exemple à scipy peut être utile https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-438522881 )
  
  

Ensuite, il y a tous les problèmes d'incohérences entre euclidien, sqeuclidean, minkowski, etc.

Pour ce qui est des précisions, @jeremiedbb , @amueller et moi avons eu une discussion rapide, principalement en train de traire Jeremie pour son expertise. Il est d'avis que nous n'avons pas besoin de nous soucier autant des problèmes d'instabilité dans un contexte de ML en grandes dimensions dans float64. Jérémie a également laissé entendre qu'il est difficile de trouver un test efficace pour savoir si de bons résultats ont été renvoyés (cf. # 12142)

Je pense donc que nous sommes heureux avec @rth « s précédent commentaire avec le float32 pour coulée en source. Puisque cdist effectue également des upcasts vers float64, nous pourrions réimplémenter cdist pour prendre float32 (mais avec des accumulateurs float64?), Ou utiliser la segmentation, si nous voulons moins de copie dans float32 de faible intensité.

@Celelibi veut-il changer le PR dans # 11271, ou quelqu'un d'autre (l'un de nous?) Devrait-il produire une pull request complète?

Et une fois que cela a été corrigé, je pense que nous devrions faire en sorte que sqeuclidean et minkowski (p dans {0,1}) utilisent nos implémentations. Nous n'avons pas discuté de divergence avec NearestNeighbors. Un autre sprint :)

Après une brève discussion lors du sprint, nous nous sommes retrouvés de la manière suivante:

• dans le cas de grande dimension (> 32 ou> 64 choisissez le meilleur): upcast par chunks vers float64 quand il est float32 et gardez la méthode 'rapide'. Pour ce genre de données, les problèmes numériques, sur float64, sont quasiment négligeables (je vais vous fournir des benchmarks pour cela)

• dans le cas de faible dimension: implémentez le calcul sécurisé (au lieu d'utiliser scipy cdist à cause de l'upcast) dans sklearn.

(Il est tentant de lancer le upcasting float32 dans 0.20.3 également)

Voici quelques points de repère pour la comparaison de vitesse entre scipy et sklearn.
[... snip ...]

C'est très intéressant. Je ne m'attendais pas vraiment à ce résultat. J'ai refait votre benchmark et j'ai trouvé un résultat très similaire. Sauf que je préconiserais une limite inférieure de décision. Mon benchmark suggérerait 8 fonctionnalités.

Le prix à payer pour se tromper n'est pas symétrique. cdist n'est meilleur que pour les calculs d'une durée inférieure à quelques secondes et il ralentit très vite lorsque le nombre de fonctionnalités augmente. Alors, mieux vaut utiliser l'implémentation BLAS en cas de doute.

Edit: Ce benchmark était pour float64, mais je trouve également que la remontée des matrices float32 vers float64 n'ajoute à peine que quelques pour cent au temps total et ne change pas la conclusion.

J'ai remarqué que le seuil dépend de la machine sur laquelle vous exécutez les benchmarks. Je soupçonne que cela peut avoir à voir avec les instructions AVX. J'ai réalisé que les benchmarks que j'avais publiés étaient exécutés sur une machine qui n'avait pas d'instructions AVX2, seulement AVX. Et sur une machine équipée d'AVX2, j'ai obtenu des résultats similaires aux vôtres.

Mais la question ne concerne pas seulement les performances, mais aussi la précision et il est plus probable que vous rencontriez des problèmes de précision lorsque la dimension est petite. Peut-être 16 est-il un bon compromis. Qu'est-ce que tu penses ?

En ce qui concerne cette discussion, je dirais que nous devons évaluer l'exactitude pour prendre une décision éclairée.

Cependant, en ce qui concerne votre PR, l'exactitude ne devrait plus être un problème. Mais au prix d'un calcul un peu plus cher. Par conséquent, le seuil devrait probablement être décidé en comparant votre PR.

La précision de l'analyse comparative n'est pas si simple. Parce que les cas difficiles ne seront pas uniformément répartis.
Et cela peut être problématique si cela se produit sans être détecté dans un cas d'angle. Habituellement, vous voudrez avoir une précision numérique garantie dans des limites de CPU abordables.
Mais comme mentionné ailleurs, une seule fonctionnalité avec 10000000.01 et 10000000.00 devrait être suffisante pour déclencher une instabilité numérique avec fp64 lors de l'utilisation de l'équation problématique connue, 10000 et 10001 avec fp32. Avec 1024 fonctionnalités, essayez

>>> import sklearn.metrics.pairwise as sk, scipy.spatial.distance as sp
>>> X = [[10000.01] * 1024, [10000.00] * 1024]
>>> print(sk.euclidean_distances(X,X), "\n", sp.cdist(X,X))
[[ 0.          0.31895195]
 [ 0.31895195  0.        ]] 
 [[ 0.    0.32]
 [ 0.32  0.  ]]

(c'était en utilisant 0.19.1) La distance correcte est 0.32.

Comme vous pouvez le voir, les instabilités numériques ont tendance à s'aggraver avec le nombre de fonctionnalités (sauf si vos données sont rares). Ici, le résultat a moins de deux chiffres de précision avec FP64.

13410 ne résout pas ce cas particulier. c'est à dire float64 + haute dimension.

Il le corrige cependant pour float32.

Mais nous avons décidé que pour float64 + high dim, nous le gardons tel quel, car les problèmes de précision sont très peu probables et ne s'appliquent pas vraiment aux cas d'utilisation de l'apprentissage automatique.

Dans votre exemple, X [0] et X [1] ont des normes égales à 320000,32 et 320000 et leur distance est de 0,32, soit 1e-6 fois leur norme. En apprentissage automatique, les 16 chiffres significatifs (dans float64) ne sont pas tous pertinents.

Mais nous avons décidé que pour float64 + high dim, nous le gardons tel quel, car les problèmes de précision sont très peu probables et ne s'appliquent pas vraiment aux cas d'utilisation de l'apprentissage automatique.

Je serais plus modéré sur celui-ci. La réduction de la dimensionnalité est une première étape habituelle dans le ML. MDS peut être utilisé pour cela, et il fait un usage intensif de la matrice de distance euclidienne.

Si quelqu'un souhaite améliorer la précision du cas float64, il existe un moyen d'utiliser deux flottants pour représenter les résultats intermédiaires. Bien que je pense que cela commence à sortir du cadre de scikit-learn.
ftp://ftp.math.ethz.ch/users/wpp/CELL/qd.pdf

Je n'étais pas clair. Je ne dis pas que les données de haute dimension ne s'appliquent pas à l'apprentissage automatique. Je dis que le genre de problèmes de précision qui se produisent dans float64 implique des points dont la distance est de 6 ordres de grandeur inférieure à leurs normes. Avoir une telle précision n'a aucun sens dans un modèle d'apprentissage automatique réaliste

En apprentissage automatique, les 16 chiffres significatifs (dans float64) ne sont pas tous pertinents.

Je ne suis pas du tout convaincu que ce soit généralement vrai.

Dans cet exemple, nous avons perdu 15 des 16 chiffres en précision. Je serais d'accord si nous utiliserions la moitié de la précision, mais nous n'avons pas une telle relation. La perte du downcasting FP64 vers FP32 peut souvent être tolérable en raison de la précision de la mesure. Et les GPU grand public sont beaucoup plus rapides avec FP32 qu'avec FP64, par exemple (dans certains cas, ils autorisent maintenant les données FP32 et les accumulateurs FP64), et pour l'inférence de réseaux neuronaux, vous pouvez même voir int8 maintenant. Mais cela ne vaut pas partout.

Par exemple, dans le clustering k-means, il y a l'hypothèse que les clusters diffèrent considérablement dans leurs moyennes (et que nous ne connaissons pas les moyennes à l'avance), et donc nous avons ici une perte de précision. Si vous avez de nombreux clusters, certaines de leurs normes peuvent être importantes par rapport à leur séparation.
De plus, après les premières itérations initiales, ses différences de distance souvent faibles font basculer un point vers un autre cluster. La perte de précision ici peut affecter les résultats et provoquer une instabilité.
Considérons maintenant les k-moyennes sur des fragments de séries temporelles avec de nombreuses variables.

Avec l'augmentation de la taille des données, nous devons supposer que les distances au voisin le plus proche deviennent plus petites, et à moins que vos normes ne soient égales à 0, elles finiront par être plus petites que les normes vectorielles et poseront des problèmes. Cela deviendra donc probablement plus grave avec l'augmentation de la taille des ensembles de données. La malédiction de la dimensionnalité dit que les distances les plus grandes et les plus petites se ressemblent de plus en plus; Ainsi, pour calculer le classement correct du voisin le plus proche, nous pouvons avoir besoin d'une bonne précision dans les données de grande dimension. Sur l'ensemble de données 20news, la plus petite distance non nulle est d'environ 0,02 (les normes sont toutes 1). Mais ce ne sont que 10 000 instances et des contenus assez divers. Supposons maintenant que l'ensemble de données concernait plutôt une détection quasi-dupliquée ...

Je ne serais pas sûr que ce "improbable" se produise dans ML ... bien sûr, cela n'affectera pas tout le monde.

Quand je dis "Dans l'apprentissage automatique, les 16 chiffres significatifs (dans float64) ne sont pas tous pertinents.", Je ne parle pas de la distance calculée, je parle des données X.
Dans l'apprentissage automatique, vos données proviennent d'une mesure, et il n'y a pas de mesure précise au 9ème chiffre (à part très peu de mesures en physique des particules).
Donc, dans votre exemple de 10000000.01 et 10000000.00 , comment accorderiez-vous de l'importance à une distance de 0,01 lorsque votre incertitude sur les valeurs de X est bien plus grande?

Pour KMeans, il existe d'abord un moyen de surmonter une grande partie des pertes de précision. Lorsque vous recherchez le centre le plus proche d'une observation x, vous n'avez pas besoin d'ajouter la norme de x au calcul de distance, ce qui évite l'annulation catastrophique dans la plupart des cas.
Ensuite, kmeans clusters basés sur les distances euclidiennes. Mais vous ne savez pas si c'est la manière exacte dont vos données sont collectées. En fait, il y a 0 probabilité que vos données soient regroupées de cette façon. Kmeans donne une estimation de la façon dont vos données pourraient être regroupées et les points qui sont à la frontière de 2 groupes ne peuvent certainement pas être considérés comme appartenant avec certitude à l'un ou à l'autre. Quelle est votre interprétation d'un point à la même distance de 2 clusters? Le mien est que les 2 clusters ne devraient être qu'un seul cluster ou KMeans n'est pas le meilleur algorithme pour regrouper mes données (ou même kmeans me donne une assez bonne idée de la façon dont mes données sont regroupées mais je sais que les frontières des clusters ne sont pas pertinentes).

L'utilisation de "| b | ^ 2-2ab" seulement n'a pas d'annulation catastrophique - mais la même perte de précision dans les chiffres qui font la différence. Les résultats sont les mêmes que si vous ajoutiez la norme de a à chaque distance par la suite; si les distances sont beaucoup plus petites que la norme de a, alors vous obtenez une perte de précision qui est évitable en effectuant les calculs de manière traditionnelle sans hacks BLAS.
Vous ne pouvez donc PAS surmonter le problème numérique de cette façon!

K-means est un problème d'optimisation. Ainsi, de tels hacks peuvent signifier que sklearn ne trouve que des solutions pires que d'autres outils. Et comme indiqué précédemment, cela peut également provoquer des instabilités. Dans le pire des cas, cela pourrait amener sklearn kmeans à parcourir les mêmes états jusqu'à max_iter sans amélioration (en supposant que tol = 0, si vous voulez trouver un optimum local), ce que la théorie dirait est impossible.
Tant que k-means n'a pas convergé, vous ne pouvez pas en dire beaucoup sur les points avec la «même» distance à deux clusters. La prochaine itération, les moyens peuvent avoir bougé et la différence pourrait devenir beaucoup plus grande et importante!
Je ne suis pas un grand fan de k-means car cela ne fonctionne pas très bien sur des données bruyantes. Mais il existe des variantes qui gèrent mieux ces cas. Mais néanmoins, si vous l'utilisez, vous devriez probablement essayer d'obtenir la pleine qualité (c'est pourquoi j'utilise aussi toujours tol=0 ) et ne pas l'aggraver. C'est assez bon marché pour faire les bons calculs (et, comme mentionné, les problèmes s'aggravent avec la taille des données - donc pour les petites données, le temps d'exécution plus lent n'a généralement pas d'importance, pour des ensembles de données plus grands, la précision devient probablement plus importante).

Selon l'application, la différence entre 10000000.01 et 10000000.00 peut être importante. Et comme je l'ai déjà montré, si vous utilisez plusieurs fonctionnalités, les problèmes surviennent plus tôt. Avec fp32 aussi peu que 10000 et 10001 avec une seule fonctionnalité et 100 contre 101 avec 100 fonctionnalités, je suppose:

Comme mentionné, la moyenne peut avoir une signification physique que vous ne voulez pas perdre. Si vous avez des données avec des températures en Kelvin, vous ne voulez pas les mettre à l'échelle 0: 1 ou les centrer; cela ruinerait votre échelle de ratio . Maintenant, si vous souhaitez comparer, par exemple, des séries chronologiques de la température de certains produits en acier lors de leur refroidissement, et déterminer si le processus de refroidissement affecte la fiabilité de votre produit en acier. Vous avez peut-être des températures supérieures à 700 K et la série chronologique peut contenir des centaines de points de données si vous souhaitez analyser le processus de refroidissement. Même avec seulement 5 chiffres de précision d'entrée (0,01 K) avec la longueur de la série chronologique, le problème numérique peut se produire. Vous pouvez à nouveau vous retrouver avec seulement 1 à 2 chiffres dans le résultat. Je ne pense pas que vous puissiez simplement exclure que la précision compte jamais en ML si vous avez ce genre d'effet catastrophique. C'est différent si vous pouvez garantir de toujours obtenir, disons 10 chiffres sur 16 avec précision. Ici, vous ne pouvez pas faire cela, vous pouvez avoir 0 chiffres dans le pire des cas (c'est pourquoi c'est catastrophique).

Dans l'apprentissage automatique, vos données proviennent d'une mesure, et il n'y a pas de mesure précise au 9ème chiffre (à part très peu de mesures en physique des particules).

Les valeurs brutes du monde réel ont rarement ce genre de précision, c'est vrai. Mais ML ne se limite pas à ce type d'entrée. On pourrait vouloir appliquer le ML à des problèmes mathématiques, comme appliquer MDS sur le graphique d'un puzzle en forme de cube de rubik ou regrouper les stratégies réussies trouvées par votre essaim d'agents RL jouant à pacman.
Même si la source initiale des informations est le monde réel, il peut y avoir un traitement à mi-chemin qui rend la plupart des chiffres pertinents pour l'algorithme de clustering. Comme le résultat d'une descente de gradient sur une fonction dont les paramètres sont échantillonnés statistiquement dans le monde réel.

Je me demande en fait pourquoi nous en discutons encore. Je suppose que nous sommes tous d'accord pour dire que scikit-learn devrait faire de son mieux dans le compromis entre précision et temps de calcul. Et quiconque n'est pas satisfait de l'état actuel doit soumettre une pull request.

L'utilisation de "| b | ^ 2-2ab" seulement n'a pas d'annulation catastrophique - mais la même perte de précision dans les chiffres qui font la différence. Les résultats sont les mêmes que si vous ajoutiez la norme de a à chaque distance par la suite; si les distances sont beaucoup plus petites que la norme de a, alors vous obtenez une perte de précision qui est évitable en effectuant les calculs de manière traditionnelle sans hacks BLAS.
Vous ne pouvez donc PAS surmonter le problème numérique de cette façon!

Il y a une perte de précision, mais cela ne peut pas provoquer une annulation catastrophique (du moins quand a et b sont proches), et vous pouvez montrer que l'erreur relative sur la distance (qui n'est pas une distance) reste petite.
Dans le cas de KMeans où vous êtes uniquement intéressé par la recherche du centre le plus proche, vous avez suffisamment de précision pour garder la commande correcte. Si à la fin vous voulez l'inertie, alors vous pouvez simplement calculer les distances de chaque point à son centre de cluster avec la formule exacte.

De plus, KMeans n'est pas un problème d'optimisation convexe, donc même si vous le laissez fonctionner avec tol = 0 jusqu'à la convergence, vous vous retrouvez dans un minima local qui peut être très éloigné des minima globaux (même avec l'initialisation kmeans ++). Je préfère donc exécuter kmeans plusieurs fois avec des init différentes et un nombre raisonnablement petit d'itérations. Vous aurez de meilleures chances de vous retrouver dans de meilleurs minima locaux. Ensuite, vous pouvez réexécuter le meilleur jusqu'à la convergence.

L'erreur relative par rapport à la distance réelle peut être arbitraire et entraîner des voisins les plus proches erronés. Considérons le cas où | a | ² = | b | ² = 1, par exemple sur tf-idf. Supposons que les vecteurs soient très proches. Alors ab est également proche de 1, et à ce stade, vous avez déjà perdu une grande partie de votre précision.
Comme je l'ai écrit ci-dessus, l'erreur est là, même si vous n'avez pas d'annulation catastrophique. Considérez 8 chiffres de précision. La distance réelle peut être de 0,000012345678 et peut être calculée avec huit chiffres en utilisant FP32 et la distance euclidienne régulière. Mais avec cette équation, vous calculez la valeur ab = 0,99998765432 à la place, qui avec FP32 sera tronquée à environ 0,99998765 au mieux, vous avez donc perdu trois chiffres de précision inutilement dans cet exemple. La perte est aussi grande que dans le cas catastrophique. Si les distances sont beaucoup plus petites que les normes, votre précision peut devenir arbitrairement mauvaise avec cette approche.

Oui, kmeans n'est pas convexe. Mais alors vous voudrez au moins trouver un optimum local , et ne pas rester bloqué (ou même osciller car les erreurs qui en résultent se comportent de manière erratique) car votre précision est trop faible. Vous avez donc au moins une chance de trouver le global dans des cas bien élevés et avec plusieurs tentatives.

J'apprécie cette discussion, mais ce dont nous avons vraiment besoin, c'est d'une solution qui n'est pas pire que ce que nous faisions avant d'arrêter de remonter les choses vers float64. En ce sens, la solution de coulée en source » @Celelibi était suffisante. Utiliser la solution exacte en petites dimensions est une amélioration supplémentaire par rapport à ce que nous faisions auparavant.

Concernant une future version, vous sentez-vous plus en confiance pour détecter efficacement quand on pourrait envisager le calcul exact en grandes dimensions?

J'ai exécuté un benchmark pour évaluer la précision moyenne du cas float64 avec des nombres aléatoires. Je compare 3 algorithmes: neumaier_sum((x-y)**2) , numpy.sum((x-y)**2) et X2 - 2*X.dot(Y.T) + Y2.T . Le résultat exact à comparer a été obtenu en utilisant mpmath avec une précision de 256 bits.
X et Y ont 100 échantillons et un nombre variable de fonctionnalités et sont remplis de nombres aléatoires entre -2 et 2.

Sur le gif suivant, il y a une image par nombre d'entités (entre 1 et 200). Sur chaque image, chaque point représente l'erreur relative de la distance euclidienne au carré entre l'une des 10000 paires de vecteurs de X et Y . L'erreur relative est multipliée par 2 ^ 53 pour la lisibilité, ce qui correspond à peu près à l'unité ULP.
Les courbes ci-dessus sont la distribution approximative (en utilisant une estimation de la densité du noyau).

Notez que les graphiques ont été coupés à 6 ULP pour plus de lisibilité. Il montre le cas moyen, pas le pire. L'erreur de la formule développée peut devenir assez importante.

Mon analyse de ce résultat est qu'en moyenne, l'erreur relative de la formule développée peut être très grande avec peu de fonctionnalités, mais devenir rapidement similaire à celle de la différence et de la somme numpy. Le seuil étant compris entre 5 et 10 caractéristiques.

J'essaie également actuellement de trouver une limite supérieure pour l'erreur de la formule développée ainsi que des exemples pathologiques.

Je pense que la préoccupation de @ kno10 est que nous nous intéressons souvent aux cas où
les points ne sont pas distribués au hasard, mais sont proches les uns des autres ou ont une unité
norme.

En effet, mais j'avais besoin d'être convaincu qu'en pratique, ce n'est pas un BS complet. ^^

Pour compléter le commentaire ci-dessus: l'erreur relative de la formule x²+y²-2ab semble être illimitée. Sauf si mon analyse est erronée, lorsque x et y sont proches l'un de l'autre, l'erreur relative peut aller jusqu'à 2^(52*2) . Au moins théoriquement. En pratique, le pire des cas que j'ai trouvé est une erreur relative de 2^52+1 .

>>> a, b = (0xfffffec4d6282+1) * 2.0**(511-52), 0xfffffec4d6282 * 2.0**(511-52)
>>> a, b
(6.703903473040778e+153, 6.7039034730407766e+153)
>>> exactdiff = (a-b)**2
>>> exactdiff
2.2158278651204453e+276
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> computeddiff
-9.9792015476736e+291
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0
>>> bin(int(abs((computeddiff - exactdiff) / exactdiff)))
'0b10000000000000000000000000000000000000000000000000001'

Renverser le signe du résultat le rapprocherait en fait de la vérité. C'est l'exemple le plus dramatique que j'ai pu trouver, mais en fait, changer l'exposant dans les valeurs de a et b ne change pas l'erreur relative.

>>> a, b = (0xfffffec4d6282+1) * 2.0**(-52), 0xfffffec4d6282 * 2.0**(-52)
>>> a, b
(0.9999999266202912, 0.999999926620291)
>>> exactdiff = (a-b)**2
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0

Je pense qu'un tracé d'histogramme dans ULP aurait plus de sens que l'animation ci-dessus avec la distribution d'erreur intra-ULP. Donc, 0 erreur ULP et 1 erreur ULP sont "aussi bonnes que possible". 2 ULP est probablement inévitable en raison du sqrt. Toutes les erreurs plus importantes méritent d'être étudiées, je suppose.

Utiliser (computed - exact) / exact est raisonnable tant que exact est grand. Mais une fois que nous avons des défis numériques pour la valeur exacte, cela devient assez instable. Dans de tels cas, (computed-exact)/norm peut valoir la peine d'être utilisé à la place, c'est-à-dire en regardant la précision de nos calculs de distance par rapport aux données d'entrée, et non par rapport aux distances dérivées.
Si nous avons deux valeurs unidimensionnelles qui ne diffèrent que de 1 ULP, une erreur de 2 ULP peut sembler énorme; mais nous sommes déjà à la résolution des données d'entrée, donc les résultats sont assez instables.
Notez qu'avec plusieurs dimensions, nous pouvons obtenir une résolution plus élevée dans les données d'entrée.

Considérez les données d'entrée du type (1, 1e-16) vs (1, 2e-16) . Par exemple, si nous avons un attribut constant dans les données d'entrée, disons, un pixel blanc dans MNIST.
Avec l'équation basée sur la différence, tout ira bien, mais la version point pose des problèmes, n'est-ce pas? C'est pourquoi les expériences unidimensionnelles peuvent ne pas suffire pour étudier cela.

Je pense qu'un tracé d'histogramme dans ULP aurait plus de sens que l'animation ci-dessus avec la distribution d'erreur intra-ULP.

Je ne suis pas sûr de voir comment vous l'auriez représenté. Il y aurait un histogramme par nombre d'entités et par algorithme. Je ne peux pas faire grand-chose à côté d'un tracé 3D ou d'une animation.

Utiliser (computed - exact) / exact est raisonnable tant que exact est grand. Mais une fois que nous avons des défis numériques pour la valeur exacte, cela devient assez instable.

Je ne sais pas ce que vous entendez par instable dans ce contexte. La valeur exacte doit être calculée avec tout ce qu'il faut pour la rendre exacte.
(En parlant de cela, j'aurais dû calculer l'erreur relative avec une précision arbitraire aussi dans mon tracé, au lieu de comparer au résultat exactement arrondi. J'ai mis à jour mon tracé, les vagues étranges ont disparu.)

Dans de tels cas, (computed-exact)/norm peut valoir la peine d'être utilisé à la place, c'est-à-dire en regardant la précision de nos calculs de distance par rapport aux données d'entrée, et non par rapport aux distances dérivées.

Si je comprends bien votre idée, vous préférez comparer l'erreur absolue à l'ampleur des données d'entrée. Utilisation des normes vectorielles comme mesure agrégée de l'ampleur des entrées. Alors que l'erreur relative standard la compare à l'ampleur du résultat exact.

Je pense qu'avec cette métrique, vous essayez de capturer à quel point un algorithme est

• Il ne dit pas vraiment combien de chiffres du résultat sont inexacts.
• En fait, la plupart des algorithmes auraient un score inférieur à 1e-15. Même la formule développée (algorithme à base de points) aurait un score limité par quelque chose comme 5 ULP (entrée) (estimation approximative, je n'ai pas écrit la preuve complète).
• Et comme les deux métriques ne sont qu'une version redimensionnée de l'erreur absolue computed - exact , elles classeraient les algorithmes dans le même ordre lorsqu'ils seraient évalués sur les mêmes entrées.
  C'est donc la même chose que l'erreur relative habituelle, juste avec une interprétation de valeur moins utile (IMO).

Considérez les données d'entrée du type (1, 1e-16) vs (1, 2e-16) . Par exemple, si nous avons un attribut constant dans les données d'entrée, disons, un pixel blanc dans MNIST.
Avec l'équation basée sur la différence, tout ira bien, mais la version point pose des problèmes, n'est-ce pas? C'est pourquoi les expériences unidimensionnelles peuvent ne pas suffire pour étudier cela.

L'algorithme basé sur des points aurait une erreur relative de 1 , ce qui signifie que l'erreur est aussi grande que le résultat exact, et donc, aucun chiffre du résultat n'est correct. Et votre métrique aurait une valeur de 1e-16 ce qui signifie que par rapport à l'échelle de la norme vectorielle, seul le 16e chiffre est désactivé.
Je ne sais pas ce que vous essayez de montrer avec cet exemple.

Si nous sommes toujours préoccupés par la précision des euclidean_distances avec float64, mieux vaut probablement résumer cette discussion dans un nouveau numéro car il y a 100 commentaires ici.