Mesmos resultados com python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1:37a07cee5969, Dec  5 2015, 21:12:44) 
[GCC 4.2.1 (Apple Inc. build 5666) (dot 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1

Acontece apenas com a distância euclidiana e pode ser reproduzido usando diretamente sklearn.metrics.pairwise.euclidean_distances :

import scipy
import sklearn.metrics.pairwise

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)

# compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_32], [b_32])

np.set_printoptions(precision=200)

print(dist_64_sklearn)
print(dist_32_sklearn)

Não consegui rastrear mais o erro.
Espero que isso possa ajudar.

numpy pode usar um acumulador de maior precisão. sim é assim
merece correção.

Em 19 de julho de 2017, às 12h05, "nvauquie" [email protected] escreveu:

Mesmos resultados com python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1: 37a07cee5969, 5 de dezembro de 2015, 21:12:44)
[GCC 4.2.1 (Apple Inc. build 5666) (ponto 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1

Isso acontece apenas com a distância euclidiana e pode ser reproduzido usando
diretamente sklearn.metrics.pairwise.euclidean_distances:

importar scipy
import sklearn.metrics.pairwise

criar vetores de 64 bits a e b que são muito semelhantes entre si

a_64 = np.array ([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype = np.float64)
b_64 = np.array ([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype = np.float64)

criar versões de 32 bits de a e b

a_32 = a_64.astype (np.float32)
b_32 = b_64.astype (np.float32)

calcule a distância de a até b usando sklearn, tanto para 64 bits quanto para 32 bits

dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_32], [b_32])

np.set_printoptions (precisão = 200)

imprimir (dist_64_sklearn)
imprimir (dist_32_sklearn)

Não consegui rastrear mais o erro.
Espero que isso possa ajudar.

-
Você está recebendo isto porque está inscrito neste tópico.
Responda a este e-mail diretamente, visualize-o no GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-316074315 ,
ou silenciar o tópico
https://github.com/notifications/unsubscribe-auth/AAEz65yy8Aq2FcsDAcWHT8qkkdXF_MfPks5sPLu_gaJpZM4OXbpZ
.

Eu gostaria de trabalhar nisso, se possível

Vá em frente!

Acho que o problema está no fato de que estamos usando sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y)) para calcular a distância euclidiana
Porque se eu tentar - (-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) obtenho a resposta 0 para np.float32, enquanto obtenho o ans correto para np.float 64.

@jnothman O que você acha que devo fazer então? Conforme mencionado em meu comentário acima, o problema provavelmente está computando a distância euclidiana usando sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

Então você está dizendo que ponto está retornando um resultado menos preciso do que produto e soma?

Não, o que estou tentando dizer é que o ponto está retornando um resultado mais preciso do que o produto e a soma
-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) dá saída [[0.]]
enquanto np.sqrt(((X-Y) * (X-Y)).sum(axis=1)) dá saída [ 0.02290595]

Não está claro o que você está fazendo, em parte porque você não está postando um snippet totalmente independente.

Olhando rapidamente para sua última postagem, as duas coisas que você está tentando comparar [[0.]] e [0.022...] não têm as mesmas dimensões (talvez um problema de copiar e colar, mas novamente difícil de saber porque não tem um trecho completo).

Ok desculpe meu mal

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
X = a_64.astype(np.float32)
Y = b_64.astype(np.float32)

X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]

#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
print(np.sqrt(distances))

#Euclidean distance computed using (X-Y)^2
print(np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis]))

RESULTADO

[[ 0.03125]]
[[ 0.02290595136582851409912109375]]

O primeiro método é como ele é calculado pela função de distância euclidiana.
Também para esclarecer o que eu quis dizer acima foi o fato de que sum-then-product tem menor precisão, mesmo quando usamos funções numpy para fazê-lo

Sim, posso replicar isso. Eu vejo que fazer a subtração inicialmente
permite que a precisão da diferença seja mantida. Fazendo o ponto
produto e, em seguida, subtraindo (ou negando e adicionando), como fazemos atualmente,
perde esta precisão porque os números mais significativos são muito maiores do que
as diferenças.

A implementação atual é mais eficiente em termos de memória para um grande número de
características. Mas suponho que a distância euclidiana se torna cada vez mais irrelevante
em dimensões altas, então a memória é dominada pelo número de saídas
valores.

Portanto, voto pela adoção de uma implementação mais estável numericamente ao longo do
implementação d-assintoticamente eficiente que temos atualmente. Uma opinião,
@ogrisel? @agramfort?

E isso é mais preocupante, já que recentemente permitimos float32s
para ser mais comum entre os estimadores.

Portanto, para este exemplo product-then-sum funciona perfeitamente bem para np.float64, então uma possível solução poderia ser converter a entrada para float64, calcular o resultado e retornar o resultado convertido de volta para float32. Eu acho que isso seria mais eficiente, mas não tenho certeza se funcionaria bem para algum outro exemplo.

converter para float64 não será mais eficiente no uso de memória do que
subtração.

Oh sim, você está certo, desculpe por isso, mas acho que usar float64 e, em seguida, fazer product-then-sum seria mais eficiente computacionalmente, se não em relação à memória.

E a razão para usar product-then-sum era ter mais eficiência computacional e não eficiência de memória.

claro, mas não acredito que haja qualquer razão para supor que seja de fato
mais eficiente computacionalmente, exceto por não ter que realizar um
matriz intermediária. Assumindo que limitamos a memória de trabalho absoluta (por exemplo, por
fragmentação), por que pegar o produto escalar, duplicando e subtraindo normas
ser muito mais eficiente do que subtrair e elevar ao quadrado?

Fornece benchmarks?

Ok, então eu criei um script Python para comparar o tempo gasto pela subtração e depois ao quadrado e conversão para float64 e depois produto-e-soma e descobrimos que se escolhermos um X e Y como vetores muito grandes, os 2 resultados serão muito diferentes . Além disso, @jnothman você acertou, subtração e quadratura é mais rápido.
Aqui está o script que escrevi, se houver algum problema, por favor me avise

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
from timeit import default_timer as timer

for i in range(9):
    X = np.random.rand(1,3 * (10**i)).astype(np.float32)
    Y = np.random.rand(1,3 * (10**i)).astype(np.float32)

    X, Y = check_pairwise_arrays(X, Y)
    XX = row_norms(X, squared=True)[:, np.newaxis]
    YY = row_norms(Y, squared=True)[np.newaxis, :]

    #Euclidean distance computed using product-then-sum
    distances = safe_sparse_dot(X, Y.T, dense_output=True)
    distances *= -2
    distances += XX
    distances += YY

    ans1 = np.sqrt(distances)

    start = timer()
    ans2 = np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis])
    end = timer()
    if ans1 != ans2:
        print(end-start)

        start = timer()
        X = X.astype(np.float64)
        Y = Y.astype(np.float64)
        X, Y = check_pairwise_arrays(X, Y)
        XX = row_norms(X, squared=True)[:, np.newaxis]
        YY = row_norms(Y, squared=True)[np.newaxis, :]
        distances = safe_sparse_dot(X, Y.T, dense_output=True)
        distances *= -2
        distances += XX
        distances += YY
        distances = np.sqrt(distances)
        end = timer()
        print(end-start)
        print('')
        if abs(ans2 - distances) > 1e-3:
            # np.set_printoptions(precision=200)
            print(ans2)
            print(np.sqrt(distances))

            print(X, Y)
            break

vale a pena testar como ele se dimensiona com o número de amostras, não apenas o
número de recursos ... tomar normas pode ter a vantagem de computar alguns
coisas uma vez por amostra, não uma vez por par de amostras

Em 20 de outubro de 2017, 02:39, "Osaid Rehman Nasir" [email protected]
escrevi:

Ok, então criei um script python para comparar o tempo gasto por
subtração e depois ao quadrado e conversão para float64 e depois produto e soma
e acontece que se escolhermos um X e Y como vetores muito grandes, então os 2
os resultados são muito diferentes. Também @jnothman https://github.com/jnothman
você estava certo, subtração e quadratura é mais rápido.
Aqui está o script que escrevi, se houver algum problema, por favor me avise

importar numpy como np
importar scipy
de sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
de sklearn.utils.extmath import safe_sparse_dot
from timeit importar default_timer como cronômetro

para i no intervalo (9):
X = np.random.rand (1,3 * (10 i)). Astype (np.float32)Y = np.random.rand (1,3 * (10 i)). Astype (np.float32)

X, Y = check_pairwise_arrays (X, Y)
XX = row_norms (X, squared = True) [:, np.newaxis]
YY = row_norms (Y, ao quadrado = True) [np.newaxis,:]

# Distância euclidiana calculada usando produto-então-soma
distâncias = safe_sparse_dot (X, YT, dense_output = True)
distâncias * = -2
distâncias + = XX
distâncias + = YY

ans1 = np.sqrt (distâncias)

iniciar = cronômetro ()
ans2 = np.sqrt (row_norms (XY, squared = True) [:, np.newaxis])
fim = temporizador ()
se ans1! = ans2:
imprimir (fim-início)

  start = timer()
  X = X.astype(np.float64)
  Y = Y.astype(np.float64)
  X, Y = check_pairwise_arrays(X, Y)
  XX = row_norms(X, squared=True)[:, np.newaxis]
  YY = row_norms(Y, squared=True)[np.newaxis, :]
  distances = safe_sparse_dot(X, Y.T, dense_output=True)
  distances *= -2
  distances += XX
  distances += YY
  distances = np.sqrt(distances)
  end = timer()
  print(end-start)
  print('')
  if abs(ans2 - distances) > 1e-3:
      # np.set_printoptions(precision=200)
      print(ans2)
      print(np.sqrt(distances))

      print(X, Y)
      break

-
Você está recebendo isso porque foi mencionado.
Responda a este e-mail diretamente, visualize-o no GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-337948154 ,
ou silenciar o tópico
https://github.com/notifications/unsubscribe-auth/AAEz6z5o2Ao_7V5-Lflb4HosMrHCeOrVks5st209gaJpZM4OXbpZ
.

de qualquer forma, você gostaria de enviar um PR, @ragnerok?

sim claro, o que você quer que eu faça?

fornecer uma implementação mais estável, também um teste que falharia no
implementação atual, e idealmente um benchmark que mostra que não perdemos
muito da mudança, em casos razoáveis.

Queria perguntar se é possível encontrar a distância entre cada par de linhas com vetorização. Não consigo pensar em como fazer isso vetorizado.

Você quer dizer diferença (não distância) entre pares de linhas? Claro que você pode fazer isso se estiver trabalhando com matrizes entorpecidas. Se você tem arrays com formas (n_samples1, n_features) e (n_samples2, n_features), você só precisa reformulá-lo para (n_samples1, 1, n_features) and (1, n_samples2, n_features) e fazer a subtração:

>>> X = np.random.randint(10, size=(10, 5))
>>> Y = np.random.randint(10, size=(11, 5))
X.reshape(-1, 1, X.shape[1]) - Y.reshape(1, -1, X.shape[1])

Sim, obrigado, isso realmente ajudou 😄

Também gostaria de perguntar se eu fornecer uma implementação mais estável, não usarei X_norm_squared e Y_norm_squared. Portanto, também os removo dos argumentos ou devo avisar que não têm qualquer utilidade?

Acho que eles serão descontinuados, mas primeiro precisamos ter certeza de que
não há nenhum caso em que devemos manter essa versão.

vamos ter muito cuidado ao mudar isso. é amplamente utilizado e
implementação de longa data. devemos ter certeza de não retardar nenhum importante
casos. podemos precisar fazer a operação em blocos para evitar memória alta
uso (que talvez seja mais complicado pelo fato de ser chamado
dentro de funções que se agrupam para minimizar a retirada de memória de saída de
distâncias em pares).

Eu realmente gostaria de ouvir de outros desenvolvedores importantes que sabem sobre computação
custos e precisão numérica ... @ogrisel , @lesteve , @rth ...

Em 5 de novembro de 2017, 5:27, "Osaid Rehman Nasir" [email protected]
escrevi:

Também gostaria de perguntar se eu fornecer uma implementação mais estável, não serei
usando X_norm_squared e Y_norm_squared. Então, eu os removo do
argumentos também ou devo avisar sobre não ter qualquer utilidade?

-
Você está recebendo isso porque foi mencionado.
Responda a este e-mail diretamente, visualize-o no GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-341919282 ,
ou silenciar o tópico
https://github.com/notifications/unsubscribe-auth/AAEz63izdpQGDEuW32m8Aob6rrsvV6q-ks5szKyHgaJpZM4OXbpZ
.

mas seria mais fácil discutir precisamente se você abrir um PR

Ok, vou abrir um PR então, com uma implementação bem básica desta função

A questão é o que deve ser feito sobre isso para a versão de 0.20. Poderia haver algumas melhorias simples / temporárias (evento ao custo, por exemplo, do uso de memória) que poderiam ser consideradas?

A solução e a análise propostas em # 11271 são definitivamente muito valiosas, mas pode exigir mais alguma discussão para ter certeza de que esta é a solução ideal. Em particular, estou preocupado com o fato de que agora temos algumas discussões pendentes sobre a memória de trabalho global ideal em https://github.com/scikit-learn/scikit-learn/issues/11506 dependendo do tipo de CPU etc. enquanto este acrescentaria mais um nível de fragmentação e a complexidade do todo estaria recebendo um pouco de controle IMO. Mas talvez seja só eu, procurando uma segunda opinião.

O que você acha que deve ser feito sobre esse problema para o lançamento @jnothman @amueller @ogrisel ?

A estabilidade supera a eficiência. Problemas de estabilidade devem ser corrigidos mesmo quando
a eficiência ainda precisa de ajustes.

o foco de working_memory era fazer coisas como silhueta com grande amostra
tamanhos funcionam. Também melhorou a eficiência, mas isso pode ser ajustado para baixo no
linha.

Eu acredito fortemente que devemos tentar obter uma correção para euclidean_distances com
float32 in. Nós o quebramos em 0,19 assumindo que poderíamos fazer
euclidean_distances funcionam em 32 bits de uma forma ingênua.

Eu concordo que precisamos de uma solução. Minha preocupação aqui não é a eficiência, mas a complexidade adicional na base de código.

Dando um passo para trás, a implementação euclidiana de scipy parece ter 10 linhas de código C e, para 32 bits, simplesmente lance-as para 64 bits. Eu entendo que não é o mais rápido, mas é conceitualmente fácil de seguir e entender. No scikit-learn, usamos o truque para tornar os cálculos mais rápidos no BLAS, então há possíveis melhorias em https://github.com/scikit-learn/scikit-learn/pull/10212 e agora a possível solução fragmentada para euclidiana distância em 32 bits.

Estou apenas procurando informações sobre qual deve ser a direção geral sobre este tópico (por exemplo, tente fazer o upstream de parte dele para o scipy etc).

scipy não parece preocupado em copiar os dados ...

Mova para 0,21 seguindo o PR.

Remover o bloqueador?

sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

é numericamente instável, se ponto (x, x) e ponto (y, y) são de magnitude semelhante a ponto (x, y) por causa do que é conhecido como cancelamento catastrófico .

Isso não afeta apenas a precisão do FP32, mas é obviamente mais proeminente e falhará muito antes.

Aqui está um caso de teste simples que mostra como isso é ruim, mesmo com precisão dupla:

import numpy
from sklearn.metrics.pairwise import euclidean_distances

a = numpy.array([[100000001, 100000000]])
b = numpy.array([[100000000, 100000001]])

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

a = numpy.array([[10001, 10000]], numpy.float32)
b = numpy.array([[10000, 10001]], numpy.float32)

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

sklearn calcula uma distância de 0 aqui ambas as vezes, em vez de sqrt (2).

Uma discussão das questões numéricas de variância e covariância - e isso trivialmente se transfere para esta abordagem de distância euclidiana acelerada - pode ser encontrada aqui:

Erich Schubert e Michael Gertz.
Computação paralela numericamente estável de (co-) variância.
In: Proceedings of the 30th International Conference on Scientific and Statistical Database Management (SSDBM), Bolzano-Bozen, Italy. 2018, 10: 1–10: 12

Na verdade, a coordenada y pode ser removida desse caso de teste, a distância correta então torna-se trivialmente 1. Fiz uma solicitação de pull que aciona este problema numérico:

    XA = np.array([[10000]], np.float32)
    XB = np.array([[10001]], np.float32)
    assert_equal(euclidean_distances(XA, XB)[0,0], 1)

Não acho que meu artigo mencionado acima forneça uma solução para este problema - apenas calcule a distância euclidiana como sqrt (sum (power ())) e é de passagem única e tem uma precisão razoável. A perda já está em usar os quadrados, ou seja, o próprio ponto (x, x) já está perdendo a precisão.

@amueller como o problema pode ser mais grave do que o esperado, sugiro adicionar novamente o rótulo do bloqueador

Obrigado por este exemplo muito simples.

A razão pela qual é implementado dessa forma é porque é muito mais rápido. Ver abaixo:

x = np.random.random_sample((1000, 1000))

%timeit euclidean_distances(x,x)
20.6 ms ± 452 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit cdist(x,x)
695 ms ± 4.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Embora o número de operações seja da mesma ordem em ambos os métodos (1,5x mais no segundo), o aumento de velocidade vem da possibilidade de usar bibliotecas BLAS bem otimizadas para multiplicação de matrizes.

Isso seria uma grande desaceleração para vários estimadores no scikit-learn.

Sim, mas apenas 3-4 dígitos de precisão com FP32 e 7-8 dígitos com FP64 causar imprecisão substancial, não é? Em particular, uma vez que tais erros tendem a amplificar ...

Bem, não estou dizendo que está tudo bem agora. :)
Estou dizendo que precisamos encontrar uma solução intermediária.
Existe um PR (# 11271) que propõe lançar em float64 para fazer os cálculos. In não corrige o problema para float64, mas oferece melhor precisão para float32.

Você tem um exemplo em que usar um estimador que usa distância_euclidiana dá resultados errados devido à perda de precisão?

Eu certamente ainda acho que isso é um grande negócio e deve ser um bloqueador para 0,21. Foi um problema introduzido para 32 bits no 0.19, e não é uma boa situação deixar. Eu gostaria que tivéssemos resolvido isso antes em 0,20, e eu estaria bem, ou mesmo ansioso, para ver o # 11271 fundido nesse ínterim. Os únicos problemas nesse PR que conheço são a otimização surround da eficiência da memória, que é uma grande toca de coelho.

Há muito tempo que temos essa versão "rápida", mas sempre em float64. Eu sei, @ kno10 , que tem problemas com a precisão. Você tem uma heurística boa e rápida para descobrirmos quando isso pode ser um problema e usar uma solução mais lenta, porém mais segura?

Sim, mas apenas 3-4 dígitos de precisão com FP32 e 7-8 dígitos com FP64 causam imprecisão substancial, não é?

Obrigado por ilustrar este problema com um exemplo muito simples!

Não acho que o problema seja tão difundido quanto você sugere - afeta principalmente amostras cuja distância mútua é pequena em relação às suas normas.

A figura abaixo ilustra isso, para 2e6 pares de amostras aleatórias, onde cada amostra 1D está no intervalo [-100, 100]. O erro relativo entre a implementação do scikit-learn e do scipy é plotado em função da distância entre as amostras, normalizado por suas normas L2, ou seja,

d_norm(A, B) = d(A, B) / sqrt(‖A‖₂*‖B‖₂)

(não tenho certeza se é a parametrização certa, mas apenas para obter resultados um tanto invariáveis ​​para a escala de dados),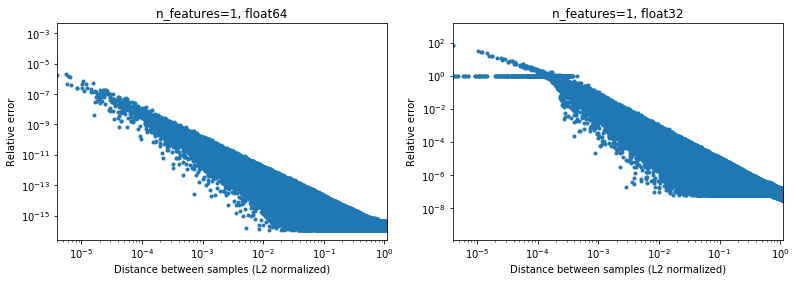

Por exemplo,

1. se tomar [10000] e [10001] a distância normalizada L2 é 1e-4 e o erro relativo no cálculo da distância será 1e-8 em 64 bits e> 1 em 32 bits (ou 1e -8 e> 1 em valor absoluto, respectivamente). Em 32 bits, este caso é realmente terrível.
2. por outro lado, para [1] e [10001] , o erro relativo será ~ 1e-7 em 32 bits, ou a precisão máxima possível.

A questão é com que frequência o caso 1. acontecerá na prática em aplicativos de ML.

Curiosamente, se formos para 2D, novamente com uma distribuição aleatória uniforme, será difícil encontrar pontos que estão muito próximos,

Claro, na realidade nossos dados não serão amostrados uniformemente, mas para qualquer distribuição devido à maldição da dimensionalidade, a distância entre quaisquer dois pontos convergirá lentamente para valores muito semelhantes (diferentes de 0) conforme a dimensionalidade aumenta. Embora seja um problema geral de ML, aqui ele pode atenuar um pouco esse problema de precisão, mesmo para dimensionalidade relativamente baixa. Abaixo dos resultados para n_features=5 ,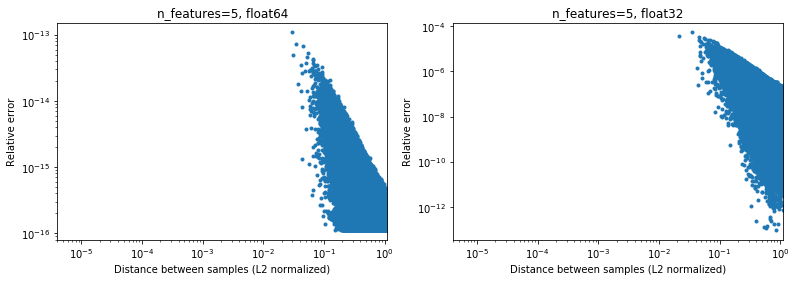
.

Portanto, para dados centralizados, pelo menos em 64 bits, pode não ser um grande problema na prática (assumindo que haja mais de 2 recursos). A aceleração computacional de 50x (conforme ilustrado acima) pode valer a pena (em 64 bits). Claro, sempre se pode adicionar 1e6 a alguns dados normalizados em [-1, 1] e dizer que os resultados não são precisos, mas eu argumentaria que o mesmo se aplica a uma série de algoritmos numéricos, e trabalhando com dados expressos no dígito significativo está apenas procurando por problemas.

(O código das figuras acima pode ser encontrado aqui ).

Qualquer abordagem rápida usando a versão ponto (x, x) + ponto (y, y) -2 Acredito que você precisará dobrar a precisão dos produtos escalares para chegar a aprox. entrada (e eu suporia que se um usuário fornecer dados float32, ele desejaria a precisão float32; com float64, ele desejaria a precisão float64). Você pode conseguir fazer isso com alguns truques (pense na soma de Kahan), mas muito provavelmente vai custar muito mais do que você ganhou inicialmente.

Eu não posso dizer quanta sobrecarga você obtém convertendo float32 em float64 durante o uso dessa abordagem. Pelo menos para float32, no meu entendimento, fazer todos os cálculos e armazenar os produtos escalares como float64 deve ser suficiente.

IMHO, os ganhos de desempenho (que não são exponenciais, apenas um fator constante) não compensam a perda de precisão (o que pode mordê-lo inesperadamente) e a maneira correta é não usar esse truque problemático. Pode, no entanto, ser possível otimizar ainda mais o código fazendo o cálculo "tradicional", por exemplo, para usar AVX. Porque sum ((xy) * 2) é quase difícil de implementar em AVX.No mínimo, eu sugeriria renomear o método para approximate_euclidean_distances , por causa da precisão às vezes baixa (que fica pior quanto mais próximos dois valores estão, o que * pode ser bom inicialmente, então comece a importar quando convergir para algum ótimo) , para que os usuários fiquem cientes desse problema.

@rth obrigado pelas ilustrações. Mas e se você estiver tentando otimizar, por exemplo, x em direção a algum ótimo. Muito provavelmente o ótimo não será zero (se fosse sempre o seu data center, a vida seria ótima) e, eventualmente, os deltas que você está computando para gradientes etc. podem ter algumas diferenças muito pequenas.
Da mesma forma, no clustering, os clusters não terão todos os seus centros próximos de zero, mas em particular com muitos clusters, x ≈ center com alguns dígitos é bem possível.

No geral, no entanto, concordo que esse problema precisa ser corrigido. Em qualquer caso, precisamos documentar os problemas de precisão da implementação atual o mais rápido possível.

Em geral, porém, não acho que essa discussão deva acontecer no scikit-learn. A distância euclidiana é usada em vários campos da computação científica e a lista de correspondência ou questões do IMO scipy é um lugar melhor para discuti-la: essa comunidade também tem mais experiência com tais questões de precisão numérica. Na verdade, o que temos aqui é um algoritmo rápido, mas um tanto aproximado. Podemos ter que implementar algumas soluções alternativas em curto prazo, mas em longo prazo seria bom saber que isso será contribuído lá.

Para 32 bits, https://github.com/scikit-learn/scikit-learn/pull/11271 pode de fato ser uma solução, só não estou muito interessado em vários níveis de fragmentação em toda a biblioteca, pois isso aumenta a complexidade do código e deseja ter certeza de que não há maneira melhor de contornar isso.

Obrigado pela sua resposta @ kno10! (Meus comentários acima não levam isso em consideração ainda) Eu responderei um pouco mais tarde.

Sim, a convergência para algum ponto fora da origem pode ser um problema.

IMHO, os ganhos de desempenho (que não são exponenciais, apenas um fator constante) não compensam a perda de precisão (o que pode mordê-lo inesperadamente) e a maneira correta é não usar esse truque problemático.

Bem, uma desaceleração> 10x para o cálculo em 64 bits terá um efeito muito real nos usuários.

Pode, no entanto, ser possível otimizar ainda mais o código fazendo o cálculo "tradicional", por exemplo, para usar AVX. Porque sum ((xy) ** 2) é quase difícil de implementar em AVX.

Tentei uma implementação rápida e ingênua com numba (que deve usar SSE),

@numba.jit(nopython=True, fastmath=True)              
def pairwise_distance_naive(A, B):
    n_samples_a, n_features_a = A.shape
    n_samples_b, n_features_b = B.shape
    assert n_features_a == n_features_b
    distance = np.empty((n_samples_a, n_samples_b), dtype=A.dtype)
    for i in range(n_samples_a):
        for j in range(n_samples_b):
            psum = 0.0
            for k in range(n_features_a):
                psum += (A[i, k] - B[j, k])**2
            distance[i, j] = math.sqrt(psum)
    return distance

obtendo uma velocidade semelhante ao scipy cdist até agora (mas não sou um especialista em numba), e também não tenho certeza sobre o efeito de fastmath .

usando a versão ponto (x, x) + ponto (y, y) -2 * ponto (x, y)

Apenas para referência futura, o que estamos fazendo atualmente é aproximadamente o seguinte (porque há uma dimensão que não aparece na notação acima),

def quadratic_pairwise_distance(A, B):
    A2 = np.einsum('ij,ij->i', A, A)
    B2 = np.einsum('ij,ij->i', B, B)
    return np.sqrt(A2[:, None] + B2[None, :] - 2*np.dot(A, B.T))

onde einsum e dot agora usam BLAS. Eu me pergunto, se além de usar o BLAS, isso também faz o mesmo número de operações matemáticas que a primeira versão acima.

Eu me pergunto, se além de usar o BLAS, isso também faz o mesmo número de operações matemáticas que a primeira versão acima.

Não. O ((x - y) * 2.sum ()) tem desempenho* n_samples_x * n_samples_y * n_features * (1 subtração + 1 adição + 1 multiplicação)
enquanto que xx + yy -2x.y desempenha
n_samples_x * n_samples_y * n_features * (1 adição + 1 multiplicação) .
Há uma proporção de 2/3 para o número de operações entre as 2 versões.

Após a discussão acima,

• Feito um PR para permitir, opcionalmente, calcular distâncias euclidianas exatamente https://github.com/scikit-learn/scikit-learn/pull/12136
• Alguns WIP para ver se podemos detectar e atenuar os pontos problemáticos em https://github.com/scikit-learn/scikit-learn/pull/12142

Para 32 bits, ainda precisamos mesclar https://github.com/scikit-learn/scikit-learn/pull/11271 de alguma forma por meio da IMO, os PRs acima são um tanto ortogonais a ele.

Para sua informação: ao corrigir alguns problemas no OPTICS e atualizar o teste para usar os resultados de referência do ELKI, eles falham com metric="euclidean" mas são bem-sucedidos com metric="minkowski" . As diferenças numéricas são grandes o suficiente para causar uma ordem de processamento diferente (apenas diminuir o limite não é suficiente).

https://github.com/kno10/scikit-learn/blob/ab544709a392e4dc7b22e9fd60c4755baf3d3053/sklearn/cluster/tests/test_optics.py#L588

Eu realmente não estou entendendo isso, mas estou surpreso que não haja uma solução existente. Este parece ser um cálculo muito comum e parece que estamos reinventando a roda. Alguém já tentou alcançar a comunidade de computação científica mais ampla?

Ainda não, mas concordo que devemos. A única coisa que descobri sobre isso no scipy foi https://github.com/scipy/scipy/pull/2815 e problemas vinculados.

Acho que @jeremiedbb pode ter uma ideia?

Infelizmente, ainda não é satisfatório :(

Gostaríamos de contar com uma biblioteca altamente otimizada para este tipo de computação, como fazemos para álgebra linear com bibliotecas BLAS, como OpenBLAS ou MKL. Mas a distância euclidiana não faz parte disso. O truque do ponto é uma tentativa de fazer isso contando com a sub-rotina de multiplicação matriz-matriz BLAS nível 3. Mas isso não é preciso e não há como torná-lo mais preciso usando o mesmo método. Temos que diminuir nossa expectativa em termos de velocidade ou precisão.

Acho que em algumas situações, a precisão total não é obrigatória e manter o método rápido é bom. É quando as distâncias são usadas para tarefas de "encontrar o mais próximo". Os problemas de precisão no método rápido aparecem quando as distâncias entre os pontos são pequenas em comparação com sua norma (em uma proporção ~ <1e-4 para flutuante 32 e ~ <1e-8 para flutuante64). Primeiro, para que essa situação aconteça, o conjunto de dados precisa ser bastante denso. Então, para ter um erro de pedido, você precisa ter os dois pontos mais próximos quase na mesma distância. Além disso, nesse caso, do ponto de vista do ML, ambos conduziriam a ajustes quase igualmente bons.

Na situação acima, há algo que podemos fazer para diminuir a frequência dessa ordenação errada (até 0?). Na situação argmin de distância de pares. Podemos mover a má ordenação para pontos que não são os mais próximos. Basicamente, usando o fato de que uma das normas não é necessária para encontrar o argmin, consulte o comentário . Possui 2 vantagens. É um mais robusto (até agora não encontrei uma ordem errada ainda) e é ainda mais rápido porque evita alguns cálculos.

Uma desvantagem, ainda na mesma situação, se no final quisermos as distâncias reais aos pontos mais próximos, as distâncias calculadas com o método acima não podem ser utilizadas. Eles são apenas parcialmente calculados e não são precisos de qualquer maneira. Precisamos recalcular as distâncias de cada ponto até o ponto mais próximo. Mas isso é rápido porque para cada ponto há apenas uma distância a ser calculada.

Eu me pergunto se o que descrevi acima cobre todos os casos de uso de euclidean_distances no sklearn. Mas sugiro fazer isso onde quer que possa ser aplicado. Para fazer isso, podemos adicionar um novo parâmetro a euclidean_distances para calcular apenas a parte necessária a fim de encadear com argmin. Em seguida, use-o em pairwise_distances_argmin e em pairwise_distances_argmin_min (recalculando as distâncias mínimas reais no final do último).

Quando não pudermos fazer isso, volte para o lento, mas preciso, ou adicione uma opção como em # 12136.
Podemos tentar otimizá-lo um pouco para diminuir a queda de desempenho porque eu concordo que este não parece ideal. Tenho algumas ideias para isso.

Outra possibilidade de continuar usando o BLAS é combinar axpy com nrm2 mas isso está longe de ser ideal. Ambas são funções BLAS de nível 1 e envolvem uma cópia. Isso só seria mais rápido na dimensão> 100.
Idealmente, gostaríamos que a distância euclidiana fosse incluída no BLAS ...

Finalmente, existe outra solução, que consiste em upcasting. Isso é feito em # 11271 para float32. A vantagem é que a velocidade é apenas metade da atual e a precisão é mantida. No entanto, isso não resolve o problema do float64. Talvez possamos encontrar uma maneira de fazer algo semelhante no cython para float64. Eu não sei exatamente como, mas usando 2 números float64 para simular um float128. Posso tentar para ver se é factível.

Idealmente, gostaríamos que a distância euclidiana fosse incluída no BLAS ...

Isso é algo que as bibliotecas considerariam? Se o OpenBLAS fizer isso, já estaremos em uma situação muito boa ...

Além disso, quais são as diferenças exatas entre nós fazendo isso e o BLAS fazendo isso? Detectar os recursos da CPU e decidir qual implementação usar ou algo parecido? Ou apenas ter compilado versões para arquiteturas mais diversas?
Ou apenas mais tempo / energia gasto escrevendo implementações eficientes?

Isso é interessante: uma implementação alternativa do método instável rápido, mas alegando ser muito mais rápido do que sklearn:
https://github.com/droyed/eucl_dist
(embora não resolva esse problema lol)

Esta discussão parece relacionada https://github.com/scipy/scipy/issues/5657

Veja o que julia faz: https://github.com/JuliaStats/Distances.jl/blob/master/README.md#precision -for-euclidean-and-sqeuclidean
Permite definir um limite de precisão para forçar o recálculo.

Respondendo minha própria pergunta: OpenBLAS tem o que parece ser uma montagem escrita à mão para cada processador (não arquitetura!) E heutística para escolher kernels para diferentes tamanhos de problema. Então eu não acho que seja uma questão de colocá-lo no openblas tanto quanto de encontrar alguém para escrever / otimizar todos aqueles kernels ...

Obrigado pelos pensamentos adicionais!

Em uma resposta parcial,

Gostaríamos de contar com uma biblioteca altamente otimizada para este tipo de computação, como fazemos para álgebra linear com bibliotecas BLAS, como OpenBLAS ou MKL.

Sim, eu também esperava que pudéssemos fazer mais disso no BLAS. A última vez que não procurei nada no BLAS API padrão parece perto o suficiente (mas não sou um especialista nisso). BLIS pode oferecer mais flexibilidade, mas como não o estamos usando por padrão, ele é de uso um tanto limitado (embora numpy possa algum dia https://github.com/numpy/numpy/issues/7372)

Veja o que julia faz: permite definir um limite de precisão para forçar o recálculo.

Ótimo saber!

Devemos abrir uma edição separada para o cálculo aproximado mais rápido vinculado acima? Parece interessante

O aumento de velocidade na CPU de x2-x4 pode ser devido a https://github.com/scikit-learn/scikit-learn/pull/10212 .

Eu prefiro abrir uma edição sobre scipy depois de estudarmos esta questão o suficiente para chegar a uma solução razoável (e então possivelmente retroceder), pois sinto que a distância euclidiana é algo básico o suficiente que deve ser do interesse de muitas pessoas fora do ML (e ao mesmo tempo ter a opinião das pessoas lá, por exemplo, sobre questões de precisão, seria útil).

É até 60x, certo?

Isso é interessante: uma implementação alternativa do método instável rápido, mas alegando ser muito mais rápido do que sklearn

hum não tenho certeza sobre isso. Eles estão fazendo um benchmarking de %timeit pairwise_distances(a,b, 'sqeuclidean') , que usa o de Scipy. Eles deveriam fazer %timeit pairwise_distances(a,b, 'euclidean', metric_params={'squared': True}) e sua aceleração não seria tão boa :)
Como mostrado no início da discussão, sklearn pode ser 35x mais rápido do que scipy

Sim, os benchmarks são apenas 30% melhores com metric="euclidean" (em vez de squeclidean ),

In [1]: from eucl_dist.cpu_dist import dist                                                                                                                  
    ... import numpy as np                                                                                                                                   
In [4]: rng = np.random.RandomState(1)                                                                                                                        
    ... a = rng.rand(1000, 300)                                                                                                                              
    ...b = rng.rand(1000, 300)                                                                                                                              

In [7]: from sklearn.metrics.pairwise import pairwise_distances                                                                                              
In [8]: %timeit pairwise_distances(a, b, 'sqeuclidean')                                                                                                      
214 ms ± 2.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [9]: %timeit pairwise_distances(a, b)                                                                                                                     
27.4 ms ± 2.48 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [10]: from eucl_dist.cpu_dist import dist                                                                                                                 
In [11]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float32')                                                                                
20.8 ms ± 330 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [12]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float64')                                                                                
20.4 ms ± 222 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Isso é algo que as bibliotecas considerariam? Se o OpenBLAS fizer isso, já estaremos em uma situação muito boa ...

Não soa direto. BLAS é um conjunto de especificações para rotinas de álgebra linear e existem várias implementações dele. Eu não sei o quão abertos eles estão para adicionar novos recursos que não estejam nas especificações originais. Para isso, talvez o blis fosse mais aberto, mas como disse antes, não é o padrão por enquanto.

Https://github.com/scikit-learn/scikit-learn/issues/12600 na manipulação de sqeuclidean vs euclidean em pairwise_distances .

Preciso de alguma clareza sobre o que queremos para isso. Queremos que pairwise_distances seja próximo - no sentido de all_close - para 'euclidiano' e 'sqeuclidiano'?

É um pouco complicado. Como x está próximo de y, não significa que x² está próximo de y². A precisão é perdida durante a quadratura.

A solução alternativa julia vinculada acima é muito interessante e simples de implementar. No entanto, suspeito que não funcione como esperado para 'sqeuclidean'. Suspeito que você tenha que definir o limite abaixo para obter a precisão desejada.

O problema de definir um limite muito baixo é que ele induz muitos recálculos e uma grande queda no desempenho. No entanto, isso é mitigado pela dimensão do conjunto de dados. O mesmo limite irá desencadear muito menos recálculos em dimensões altas (as distâncias são maiores).

Talvez possamos ter 2 implementações e alternar dependendo da dimensão do conjunto de dados. O lento, mas seguro, para os de baixa dimensão (não há muita diferença entre scipy e sklearn nesse caso) e o rápido + limiar para os de alta dimensão.

Isso vai precisar de alguns benchmarks para descobrir quando mudar e definir o limite, mas isso pode ser um vislumbre de esperança :)

Aqui estão alguns benchmarks para comparação de velocidade entre scipy e sklearn. Os benchmarks comparam sklearn.metrics.pairwise.euclidean_distances(X,X) com scipy.spatial.distance.cdist(X,X) para Xs de todos os tamanhos. O número de amostras vai de 2⁴ (16) a 2¹³ (8192), e o número de recursos vai de 2⁰ (1) a 2¹³ (8192).

O valor em cada célula é a aceleração de sklearn vs scipy, ou seja, abaixo de 1 sklearn é mais lento e acima de 1 sklearn é mais rápido.

O primeiro benchmark está usando a implementação MKL do BLAS e um único núcleo.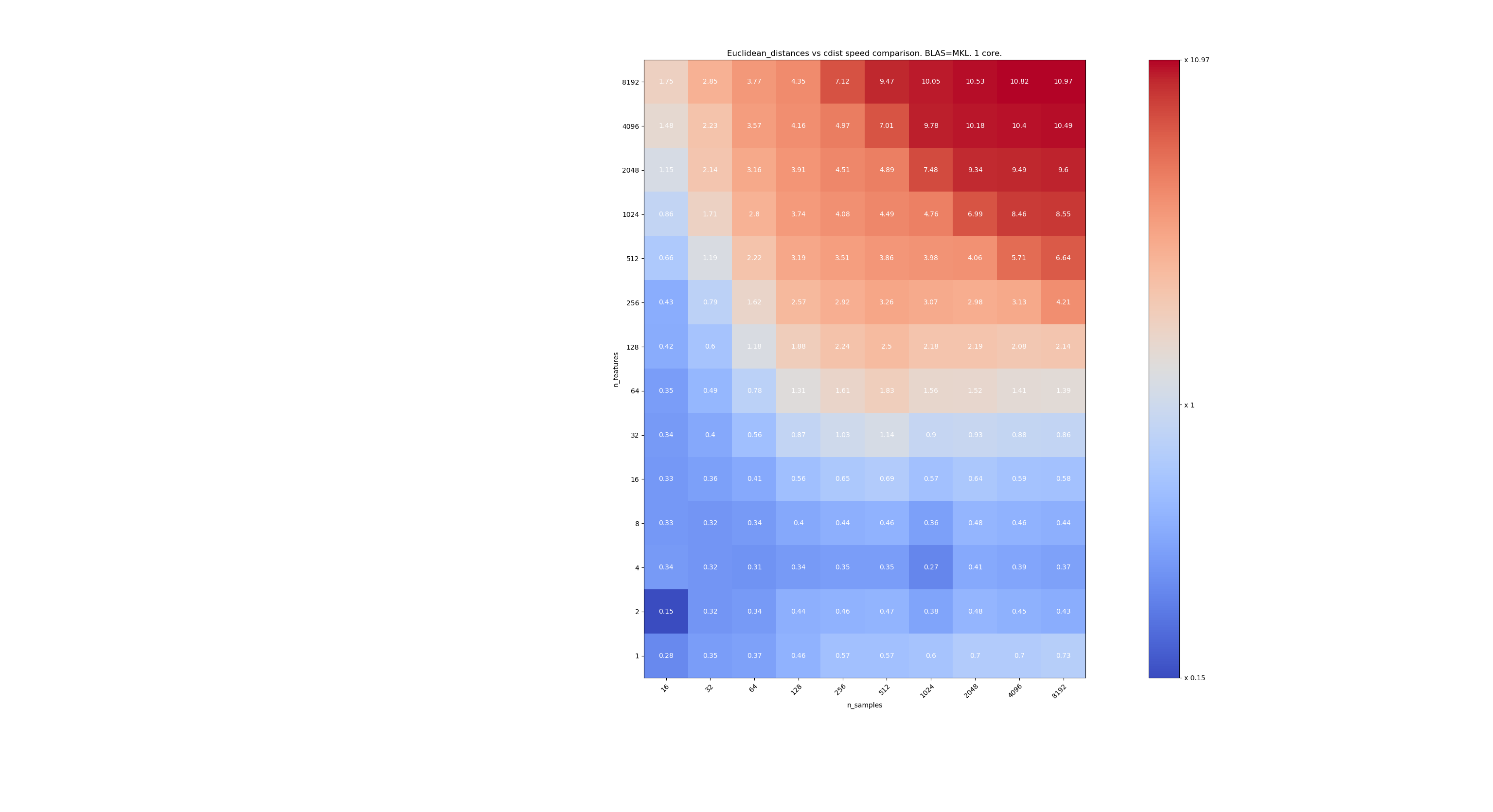

O segundo está usando a implementação OpenBLAS do BLAS e um único núcleo. É só verificar se MKL e OpenBLAS têm o mesmo comportamento.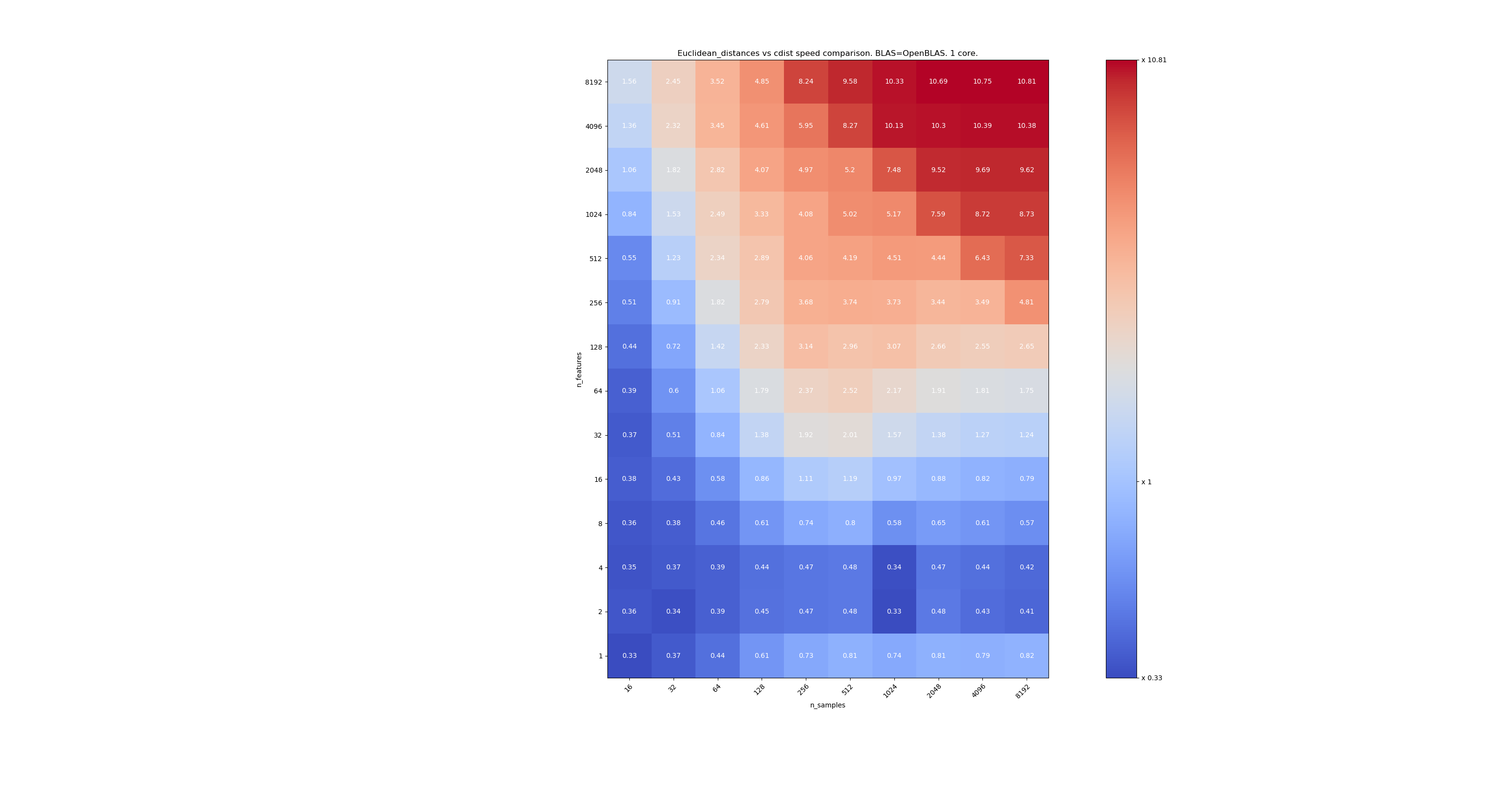

O terceiro está usando a implementação MKL de BLAS e 4 núcleos. O fato é que euclidean_distances é paralelizado por uma função BLAS NÍVEL 3, mas cdist usa apenas uma função BLAS NÍVEL 1. Curiosamente, quase não muda a fronteira.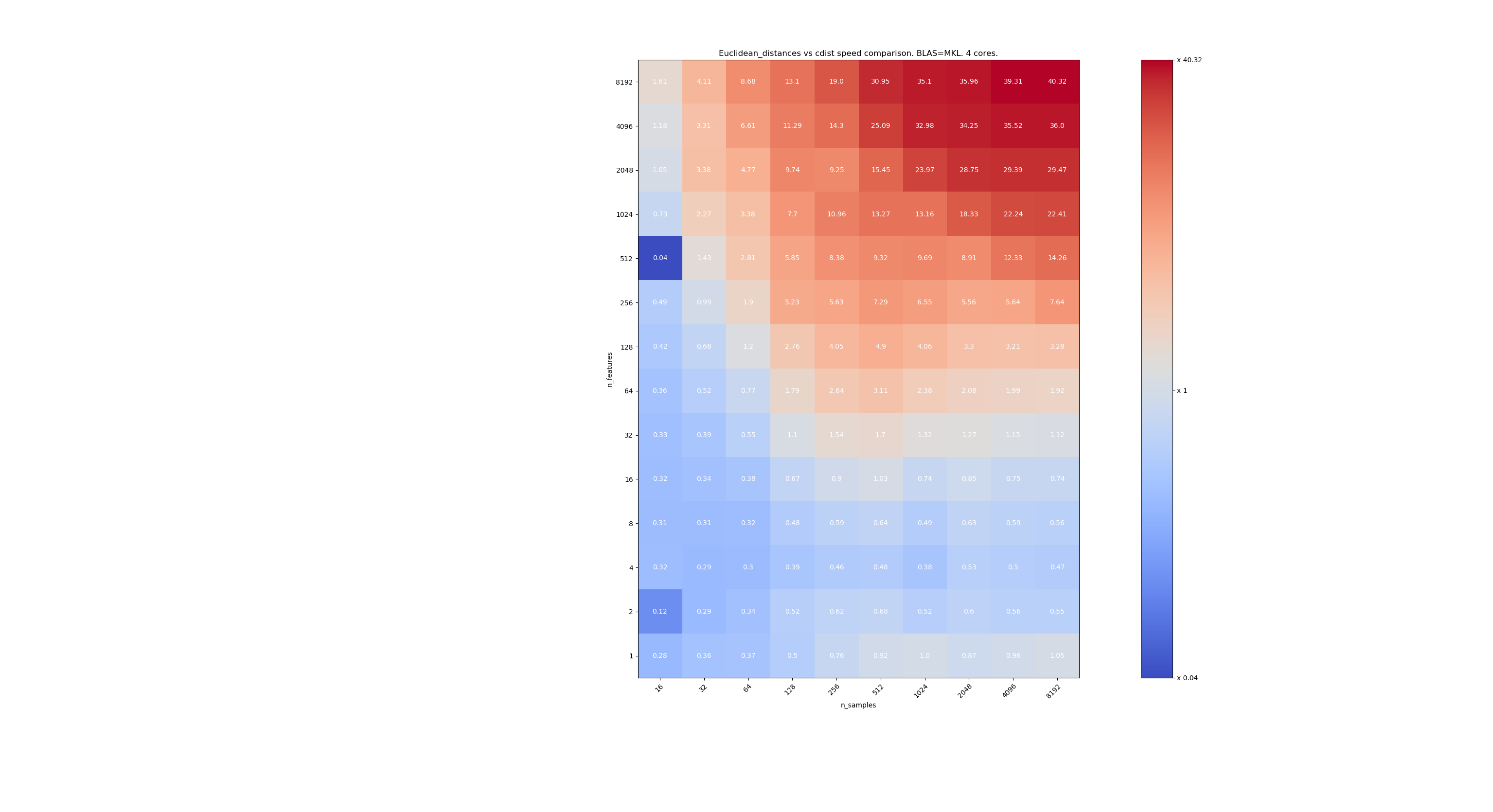

Quando n_samples não é muito baixo (> 100), parece que a fronteira está em torno de 32 recursos. Poderíamos decidir usar cdist quando n_features <32 e euclidean_distances quando n_features> 32. Isso é mais rápido e não há problema de precisão. Isso também tem a vantagem de que, quando n_features é pequeno, o limite julia leva a muitos recálculos. Usar cdist evita isso.

Quando n_features> 32, podemos manter a implementação euclidean_distances , atualizada com o limite de julia. Adicionar o limite não deve deixar euclidean_distances muito lento, porque o número de recursos é alto o suficiente para que apenas alguns recálculos sejam necessários.

@jeremiedbb ótimo, obrigado pela análise. A conclusão parece um ótimo caminho a seguir para mim.

Oh, suponho que isso foi tudo para float64, certo? O que fazemos com float32? upcast sempre? upcast para> 32 recursos?

Não li os comentários com atenção (irei em breve), apenas para sua informação que float64 tem limitações, consulte # 12128

@ qinhanmin2014 sim, a precisão do float64 tem limitações, mas é precisa o suficiente para produzir resultados fp32 confiáveis ​​pelo que posso dizer. A questão é em quais parâmetros um upcast para fp64 é realmente mais barato do que usar cdist do scipy.
Como visto nos benchmarks acima, mesmo o BLAS multi-core geralmente não é mais rápido. Isso parece ser válido principalmente para dados dimensionais elevados (mais de 64 dimensões; antes disso, o benefício geralmente não vale o esforço IMHO) - e uma vez que as distâncias euclidianas não são tão confiáveis ​​em dados densos de alta dimensão, esse caso de uso IMHO não é da maior importância . Muitos usuários terão menos de 10 dimensões. Nesses casos, o cdist geralmente parece ser mais rápido?

Oh, suponho que isso foi tudo para float64, certo?

Na verdade, é para float32 e float64 (quero dizer muito semelhante). Eu sugiro sempre usar cdist quando n_features <32.

A questão é em quais parâmetros um upcast para fp64 é realmente mais barato do que usar cdist do scipy.

O upcasting diminuirá em um fator de ~ 2, então acho que cerca de n_features = 64.

Muitos usuários terão menos de 10 dimensões.

Mas nem todos, então ainda precisamos encontrar uma solução para dados de alta dimensão.

Muito boa análise @jeremiedbb !

Para dados de baixa dimensão definitivamente faria sentido usar cdist então.

Além disso, o cdist do FYI scipy eleva float32 para float64 https://github.com/scipy/scipy/issues/8771#issuecomment -384015674, não tenho certeza se isso é devido a problemas de precisão ou algo mais.

No geral, acho que faria sentido adicionar o parâmetro "algoritmo" a euclidean_distance conforme sugerido em https://github.com/scikit-learn/scikit-learn/pull/12601#pullrequestreview -176076355, possivelmente com um padrão para "Nenhum" para que também possa ser definido por meio de uma opção global como em https://github.com/scikit-learn/scikit-learn/pull/12136.

Há também uma abordagem interessante no Eigen3 para calcular normas estáveis: https://eigen.tuxfamily.org/dox/StableNorm_8h_source.html (que eu realmente não grocei ainda)

Boa explicação, melhorou minha compreensão

Não fizemos nenhum progresso nisso no sprint e provavelmente deveríamos ... e @rth não está por aí hoje.

Posso entrar remotamente se você definir um horário. Talvez no início da tarde?

Para resumir a situação,

Para problemas de precisão em cálculos de distância euclidiana,

• no caso de baixa dimensão, como @jeremiedbb mostrou acima, provavelmente deveríamos usar cdist
• no caso de alta dimensão e float 32, poderíamos escolher entre,
  
  
  
  • fragmentação, calculando a distância em 64 bits e concatenando
  
  
  • recorrer ao cdist nos casos em que a precisão é um problema (como é uma questão em aberto - chegar, por exemplo, ao scipy pode ser útil https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-438522881 )
  
  

Depois, há todas as questões de inconsistências entre euclidiana, sqeuclidiana, minkowski, etc.

Em termos de precisão, @jeremiedbb , @amueller e eu conversamos rapidamente, principalmente apenas pedindo a Jeremie por sua experiência. Ele é de opinião que não precisamos nos preocupar tanto com os problemas de instabilidade em um contexto de ML em grandes dimensões em float64. Jeremie também deu a entender que é difícil encontrar um teste eficiente para saber se bons resultados foram retornados (cf. # 12142)

Então eu acho que nós estamos felizes com @rth do anterior comentário com o upcasting para float32. Uma vez que cdist também atualiza para float64, poderíamos reimplementar cdist para ter float32 (mas com acumuladores float64?), Ou poderíamos usar chunking, se quisermos menos cópias em float32.

@Celibi deseja alterar o PR no # 11271 ou outra pessoa (um de nós?) Deve produzir uma solicitação de pull completa?

E uma vez que isso foi corrigido, acho que devemos fazer sqeuclidean e minkowski (p em {0,1}) usar nossas implementações. Não discutimos discrepâncias com os vizinhos mais próximos. Outra corrida :)

Depois de uma rápida discussão no sprint, terminamos da seguinte maneira:

• no caso de alta dimensão (> 32 ou> 64 escolha o melhor): upcast por pedaços para float64 quando for float32 e manter o método 'rápido'. Para este tipo de dados, problemas numéricos, em float64, são quase insignificantes (irei fornecer benchmarks para isso)

• no caso de baixa dimensão: implemente a computação segura (em vez de usar scipy cdist por causa do upcast) no sklearn.

(É tentador jogar upcasting float32 em 0.20.3 também)

Aqui estão alguns benchmarks para comparação de velocidade entre scipy e sklearn.
[... recorte ...]

Isto é muito interessante. Na verdade, eu não esperava esse resultado. Refiz seu benchmark e encontrei um resultado muito semelhante. Exceto que eu advogaria por um limite de decisão inferior. Meu benchmark sugere 8 recursos.

O custo de estar errado não é simétrico. cdist é melhor apenas para cálculos que duram menos de alguns segundos e fica lento muito rápido quando o número de recursos aumenta. Portanto, é melhor usar a implementação do BLAS em caso de dúvida.

Edit: Este benchmark foi para float64, mas eu também acho que o upcasting de matrizes float32 para float64 apenas adiciona alguns por cento ao tempo total e não altera a conclusão.

Percebi que o limite depende da máquina em que você está executando os benchmarks. Suspeito que tenha a ver com as instruções do AVX. Percebi que os benchmarks que publiquei foram executados em uma máquina que não tinha instruções AVX2, apenas AVX. E em uma máquina que tem AVX2, obtive resultados semelhantes aos seus.

Mas a questão não é apenas sobre o desempenho, mas também sobre a precisão e é mais provável que haja problemas de precisão quando a dimensão é pequena. Talvez 16 seja um bom compromisso. O que você acha ?

Em relação a essa discussão, eu diria que precisamos avaliar a precisão para tomar uma decisão informada.

No entanto, no que diz respeito ao seu PR, a precisão não deve ser mais um problema. Mas ao custo de um cálculo um pouco mais caro. Portanto, o limite provavelmente deve ser decidido por meio de benchmarking seu PR.

A precisão do benchmarking não é tão fácil. Porque os casos difíceis não serão distribuídos uniformemente.
E pode ser problemático se acontecer sem ser detectado em um caso de canto. Normalmente, você desejará ter precisão numérica garantida dentro dos limites acessíveis da CPU.
Mas, como mencionado em outro lugar, um único recurso com 10000000,01 e 10000000,00 deve ser suficiente para acionar a instabilidade numérica com fp64 ao usar a equação problemática conhecida, 10000 e 10001 com fp32. Com 1024 recursos, tente

>>> import sklearn.metrics.pairwise as sk, scipy.spatial.distance as sp
>>> X = [[10000.01] * 1024, [10000.00] * 1024]
>>> print(sk.euclidean_distances(X,X), "\n", sp.cdist(X,X))
[[ 0.          0.31895195]
 [ 0.31895195  0.        ]] 
 [[ 0.    0.32]
 [ 0.32  0.  ]]

(isso estava usando 0.19.1) A distância correta é 0.32.

Como você pode ver, as instabilidades numéricas tendem a piorar com o número de recursos (a menos que seus dados sejam esparsos). Aqui, o resultado tem menos de dois dígitos de precisão com FP64.

13410 não corrige este caso específico. ou seja, float64 + dimensão alta.

Ele corrige para float32 no entanto.

Mas decidimos que para float64 + high dim, vamos mantê-lo como estava, porque os problemas de precisão são muito improváveis ​​de acontecer e não se aplicam realmente a casos de uso de aprendizado de máquina.

Em seu exemplo, X [0] e X [1] têm normas iguais a 320000,32 e 320000 e sua distância é 0,32, ou seja, 1e-6 vezes sua norma. No aprendizado de máquina, os 16 dígitos significativos (em float64) não são todos relevantes.

Mas decidimos que para float64 + high dim, vamos mantê-lo como estava, porque os problemas de precisão são muito improváveis ​​de acontecer e não se aplicam realmente a casos de uso de aprendizado de máquina.

Eu seria mais moderado neste. Reduzir a dimensionalidade é um primeiro passo usual no ML. O MDS pode ser usado para isso, e faz um uso pesado da matriz de distância euclidiana.

Se alguém quiser dar uma olhada em como melhorar a precisão do caso float64, há uma maneira de usar dois flutuadores para representar os resultados intermediários. Embora eu ache que comece a ficar além do escopo do scikit-learn.
ftp://ftp.math.ethz.ch/users/wpp/CELL/qd.pdf

Eu não fui claro. Não estou dizendo que dados de alta dimensão não se aplicam ao aprendizado de máquina. Estou dizendo que o tipo de problema de precisão que acontece em float64 envolve pontos cuja distância é 6 ordens de magnitude menor do que suas normas. Ter tal precisão não tem significado em um modelo realista de aprendizado de máquina

No aprendizado de máquina, os 16 dígitos significativos (em float64) não são todos relevantes.

Não estou absolutamente convencido de que isso seja geralmente verdade.

Neste exemplo, perdemos 15 de 16 dígitos na precisão. Eu concordaria se usássemos metade da precisão, mas não temos essa relação. A perda do downcasting FP64 para FP32 pode ser tolerável devido à precisão da medição. E as GPUs de consumo são muito mais rápidas com FP32 do que com FP64, por exemplo (em alguns casos, eles permitem dados FP32 e acumuladores FP64 agora), e para inferência de redes neurais, você pode até ver int8 agora. Mas isso não acontece em todos os lugares.

Por exemplo, em k-means clustering, há o pressuposto de que os clusters diferem substancialmente nos seus meios (e que não sabemos os meios de antemão), e, portanto, temos uma perda de precisão aqui. Se você tiver muitos clusters, algumas de suas normas podem ser grandes em comparação com sua separação.
Além disso, após as primeiras iterações iniciais, muitas vezes são pequenas diferenças de distância que fazem um ponto mudar para outro cluster. A perda de precisão aqui pode afetar os resultados e causar instabilidade.
Agora considere k-means em fragmentos de séries temporais com muitas variáveis.

Com o aumento do tamanho dos dados, devemos assumir que as distâncias até o vizinho mais próximo ficam menores e, a menos que suas normas sejam 0, elas acabarão sendo menores do que as normas vetoriais e causarão problemas. Portanto, isso provavelmente se tornará mais grave com o aumento dos tamanhos dos conjuntos de dados. A maldição da dimensionalidade diz que as distâncias maiores e menores ficam cada vez mais semelhantes; portanto, para calcular a classificação correta do vizinho mais próximo, podemos precisar de boa precisão em dados de alta dimensão. No conjunto de dados 20news, a menor distância diferente de zero é cerca de 0,02 (as normas são todas 1). Mas isso são apenas 10 mil instâncias e conteúdos bastante diversos. Agora, suponha que o conjunto de dados foi sobre detecção de quase duplicata em vez disso ...

Eu não teria certeza se esse "improvável" acontecesse no ML ... é claro que não afetará a todos.

Quando digo "No aprendizado de máquina, os 16 dígitos significativos (em float64) não são todos relevantes.", Não estou falando da distância calculada, estou falando dos dados X.
No aprendizado de máquina, seus dados vêm de uma medida, e não há medida precisa até o 9º dígito (além de muito poucas na física de partículas).
Portanto, em seu exemplo de 10000000.01 e 10000000.00 , como você daria alguma importância a uma distância de 0,01 quando sua incerteza sobre os valores de X são muito maiores?

Para o KMeans, primeiro há uma maneira de superar uma grande parte das perdas de precisão. Quando você está procurando o centro mais próximo de uma observação x, não precisa adicionar a norma de x ao cálculo da distância, o que evita o cancelamento catastrófico na maioria dos casos.
Então, clusters de kmeans com base nas distâncias euclidianas. Mas você não sabe se esta é a maneira exata como seus dados são coletados. Na verdade, há uma probabilidade 0 de que seus dados sejam agrupados dessa maneira. Kmeans fornece uma estimativa de como seus dados podem ser agrupados e pontos que estão na fronteira de 2 clusters podem definitivamente não ser considerados pertencentes com certeza a um ou outro. Qual é a sua interpretação de um ponto à mesma distância de 2 clusters? O meu é que os 2 clusters devem ser apenas um cluster ou KMeans não é o melhor algoritmo para agrupar meus dados (ou mesmo o kmeans me dá uma boa ideia de como meus dados são agrupados, mas sei que as fronteiras dos clusters não são relevantes).

O uso de apenas "| b | ^ 2-2ab" não tem cancelamento catastrófico - mas a mesma perda de precisão nos dígitos que fazem a diferença. Os resultados são os mesmos como se você adicionasse a norma de a a cada distância posteriormente; se as distâncias são muito menores do que a norma de a, você obtém uma perda de precisão que é evitável fazendo os cálculos da maneira tradicional, sem hacks do BLAS.
Portanto, você realmente NÃO pode superar o problema numérico desta forma!

K-means é um problema de otimização. Portanto, esses hacks podem significar que o sklearn encontra apenas soluções piores do que outras ferramentas. E como indicado antes, isso também pode causar instabilidades. No pior caso, isso poderia fazer com que sklearn kmeans iterassem pelos mesmos estados até max_iter sem nenhuma melhoria (assumindo tol = 0, se você quiser encontrar um ótimo local), o que a teoria diria que é impossível.
Até que o k-means tenha convergido, você não pode dizer muito sobre pontos com a "mesma" distância para dois clusters. Na próxima iteração, os meios podem ter mudado e a diferença pode se tornar muito maior e importante!
Não sou um grande fã do k-means porque ele não funciona muito bem com dados barulhentos. Mas existem variações que lidam melhor com esses casos. Mas, no entanto, se você usá-lo, provavelmente deve tentar obter a qualidade total (é por isso que eu sempre uso tol=0 ) e não torná-lo pior do que o necessário. É barato o suficiente para fazer os cálculos adequados (e, como mencionado, os problemas pioram com o tamanho dos dados - portanto, para dados pequenos, o tempo de execução mais lento geralmente não importa, para conjuntos de dados maiores a precisão se torna provavelmente mais importante).

Dependendo da aplicação, a diferença entre 10000000.01 e 10000000.00 pode ser importante. E como mostrei antes, se você usar vários recursos, os problemas surgirão antes. Com fp32 tão pouco quanto 10000 e 10001 com um único recurso e 100 vs. 101 com 100 recursos, eu acho:

Conforme mencionado, a média pode ter um significado físico que você não deseja perder. Se você tiver dados com temperaturas em Kelvin, não deseja escalá-los ou centralizá-los em 0: 1; isso arruinaria sua escala de proporção . Agora, se você quiser comparar, por exemplo, séries temporais da temperatura de algum produto de aço conforme ele esfria, e descubra se o processo de esfriamento afeta a confiabilidade do seu produto de aço. Você pode estar tendo temperaturas de mais de 700 K, e a série temporal pode ter centenas de pontos de dados se você quiser analisar o processo de resfriamento. Mesmo com apenas 5 dígitos de precisão de entrada (0,01 K) com a duração da série temporal, o problema numérico pode ocorrer. Você pode acabar novamente com apenas 1-2 dígitos no resultado. Eu não acho que você pode simplesmente descartar que a precisão seja importante no ML se você tiver esse tipo de efeito catastrófico. Seria diferente se você pudesse garantir sempre obter, digamos, 10 de 16 dígitos de precisão. Aqui você não pode fazer isso, você pode ter 0 dígito certo no pior caso (é por isso que é catastrófico).

No aprendizado de máquina, seus dados vêm de uma medida, e não há medida precisa até o 9º dígito (além de muito poucas na física de partículas).

Os valores brutos do mundo real raramente têm esse tipo de precisão, isso mesmo. Mas o ML não se limita a esse tipo de entrada. Pode-se querer aplicar ML a problemas matemáticos, como aplicar MDS no gráfico de um quebra-cabeça em forma de cubo de rubik ou agrupar as estratégias de sucesso encontradas por seu enxame de agentes RL jogando pacman.
Mesmo se a fonte inicial das informações for o mundo real, pode haver algum processamento intermediário que torna a maioria dos dígitos relevantes para o algoritmo de agrupamento. Como o resultado de uma descida gradiente em uma função cujos parâmetros são amostrados estatisticamente no mundo real.

Na verdade, estou me perguntando por que ainda estamos discutindo isso. Acho que todos concordamos que o scikit-learn deve dar o melhor de si na relação entre precisão e tempo de cálculo. E quem não estiver satisfeito com o estado atual deve enviar uma solicitação pull.

O uso de apenas "| b | ^ 2-2ab" não tem cancelamento catastrófico - mas a mesma perda de precisão nos dígitos que fazem a diferença. Os resultados são os mesmos como se você adicionasse a norma de a a cada distância posteriormente; se as distâncias são muito menores do que a norma de a, você obtém uma perda de precisão que é evitável fazendo os cálculos da maneira tradicional, sem hacks do BLAS.
Portanto, você realmente NÃO pode superar o problema numérico desta forma!

Há uma perda de precisão, mas não pode causar um cancelamento catastrófico (pelo menos quando aeb estão próximos), e você pode mostrar que o erro relativo na distância (que não é uma distância) permanece pequeno.
No caso do KMeans, onde você está interessado apenas em encontrar o centro mais próximo, você tem precisão suficiente para manter a ordem correta. Se no final você quiser a inércia, então você pode simplesmente calcular as distâncias de cada ponto ao centro do cluster com a fórmula exata.

Além disso, o KMeans não é um problema de otimização convexa, então mesmo se você deixá-lo rodar com tol = 0 até a convergência, você acaba em um mínimo local que pode estar bem longe dos mínimos globais (mesmo com inicialização kmeans ++). Portanto, prefiro executar o kmeans muitas vezes com init diferentes e um número razoavelmente pequeno de iterações. Você terá uma chance melhor de acabar em um mínimo local melhor. Então você pode executar novamente o melhor até a convergência.

O erro relativo em comparação com a distância real pode ser arbitrariamente grande e, portanto, causar vizinhos mais próximos errados. Considere o caso em que | a | ² = | b | ² = 1, por exemplo em tf-idf. Suponha que os vetores estejam muito próximos. Então ab também está próximo de 1, e neste ponto você já perdeu muito de sua precisão.
Como escrevi acima, o erro está lá, mesmo se você não tiver um cancelamento catastrófico. Considere 8 dígitos de precisão. A distância real pode ser 0,000012345678 e pode ser calculada com oito dígitos usando FP32 e distância euclidiana regular. Mas com esta equação, você calcula o valor ab = 0,999998765432, que com FP32 será truncado para aproximadamente 0,999998765 na melhor das hipóteses, então você perdeu três dígitos de precisão desnecessariamente neste exemplo. A perda é tão grande quanto no caso catastrófico. Se as distâncias forem muito menores do que as normas, sua precisão pode se tornar arbitrariamente ruim com essa abordagem.

Sim, kmeans não é convexo. Mas então você vai querer pelo menos encontrar um ótimo local e não ficar preso (ou mesmo oscilar porque os erros resultantes se comportam de maneira errática) porque sua precisão é muito baixa. Assim, pelo menos você terá a chance de encontrar o global em casos bem comportados e com várias tentativas.

Agradeço essa discussão, mas o que realmente precisamos é de uma solução que não seja pior do que a que estávamos fazendo antes de pararmos de atualizar as coisas para float64. Nesse sentido, solução upcasting 's @Celelibi era suficiente. Usar a solução exata em dimensões baixas é uma melhoria adicional em relação ao que costumávamos fazer.

Em relação a uma versão futura, você sente mais confiança para detectar com eficiência quando poderemos considerar o cálculo exato em dimensões altas?

Eu executei um benchmark para avaliar a precisão média do caso float64 com números aleatórios. Eu comparo 3 algoritmos: neumaier_sum((x-y)**2) , numpy.sum((x-y)**2) e X2 - 2*X.dot(Y.T) + Y2.T . O resultado exato para comparação foi obtido usando mpmath com uma precisão de 256 bits.
X e Y têm 100 amostras e um número variável de recursos e são preenchidos com números aleatórios entre -2 e 2.

No seguinte gif, há uma imagem por número de recurso (entre 1 e 200). Em cada imagem, cada ponto representa o erro relativo da distância euclidiana quadrada entre um dos 10.000 pares de vetores de X e Y . O erro relativo é multiplicado por 2 ^ 53 para facilitar a leitura, o que corresponde aproximadamente à unidade ULP.
As curvas acima são a distribuição aproximada (usando uma estimativa de densidade do kernel).

Observe que os gráficos foram cortados em 6 ULP para facilitar a leitura. Mostra o caso médio, não o pior caso. O erro da fórmula expandida pode crescer muito.

Minha análise desse resultado é que, em média, o erro relativo da fórmula expandida pode ser muito grande com poucos recursos, mas rapidamente se torna semelhante ao da diferença e soma numpy. O limite está entre 5 e 10 recursos.

Também estou tentando encontrar um limite superior para o erro da fórmula expandida, bem como exemplos patológicos.

Acho que a preocupação de @ kno10 é que muitas vezes estamos interessados ​​em casos onde
os pontos não são distribuídos aleatoriamente, mas estão próximos uns dos outros ou têm unidade
norma.

Sim, mas eu precisava estar convencido de que, na prática, não é um BS completo. ^^

Para completar o comentário acima: o erro relativo da fórmula x²+y²-2ab parece não ter limites. A menos que minha análise esteja errada, quando x e y estão próximos um do outro, o erro relativo pode ser de até 2^(52*2) . Pelo menos teoricamente. Na prática, o pior caso que encontrei é um erro relativo de 2^52+1 .

>>> a, b = (0xfffffec4d6282+1) * 2.0**(511-52), 0xfffffec4d6282 * 2.0**(511-52)
>>> a, b
(6.703903473040778e+153, 6.7039034730407766e+153)
>>> exactdiff = (a-b)**2
>>> exactdiff
2.2158278651204453e+276
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> computeddiff
-9.9792015476736e+291
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0
>>> bin(int(abs((computeddiff - exactdiff) / exactdiff)))
'0b10000000000000000000000000000000000000000000000000001'

Inverter o sinal do resultado o deixaria mais perto da verdade. Este é o exemplo mais dramático que eu poderia encontrar, mas na verdade alterar o expoente nos valores de a e b não altera o erro relativo.

>>> a, b = (0xfffffec4d6282+1) * 2.0**(-52), 0xfffffec4d6282 * 2.0**(-52)
>>> a, b
(0.9999999266202912, 0.999999926620291)
>>> exactdiff = (a-b)**2
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0

Acho que um gráfico de histograma em ULPs faria mais sentido do que a animação acima com a distribuição de erro dentro da ULP. Portanto, 0 erro de ULP e 1 erro de ULP são "o melhor que pode acontecer". 2 ULP provavelmente é inevitável por causa do sqrt. Quaisquer erros maiores valem a pena investigar, eu presumo.

Usar (computed - exact) / exact é razoável, desde que exata seja grande. Mas, uma vez que estamos recebendo desafios numéricos para o valor exato, isso se torna bastante instável. Nesses casos, (computed-exact)/norm pode valer a pena usar, ou seja, olhando para a precisão de nossos cálculos de distância em comparação com os dados de entrada, não em comparação com as distâncias derivadas.
Se tivermos dois valores unidimensionais que diferem apenas em 1 ULP, o erro de 2 ULP pode parecer enorme; mas já estamos na resolução dos dados de entrada, então os resultados são bastante instáveis.
Observe que, com dimensões múltiplas, podemos obter uma resolução mais alta nos dados de entrada.

Considere dados de entrada do tipo (1, 1e-16) vs. (1, 2e-16) . Por exemplo, se tivermos um atributo constante nos dados de entrada, digamos, um pixel branco em MNIST.
Com a equação baseada na diferença, isso vai funcionar, mas a versão de pontos tem problemas, não é? É por isso que experimentos unidimensionais podem não ser suficientes para estudar isso.

Acho que um gráfico de histograma em ULPs faria mais sentido do que a animação acima com a distribuição de erro dentro da ULP.

Não tenho certeza se vejo como você o teria representado. Haveria um histograma por número de recurso e por algoritmo. Não há muito que eu possa fazer além de um enredo 3D ou uma animação.

Usar (computed - exact) / exact é razoável, desde que exata seja grande. Mas, uma vez que estamos recebendo desafios numéricos para o valor exato, isso se torna bastante instável.

Não tenho certeza do que você quer dizer com instável neste contexto. O valor exato deve ser calculado com o que for necessário para torná-lo exato.
(Falando nisso, eu deveria ter calculado o erro relativo com precisão arbitrária também em meu gráfico, em vez de comparar com o resultado exatamente arredondado. Atualizei meu gráfico, as ondas estranhas desapareceram.)

Nesses casos, (computed-exact)/norm pode valer a pena usar, ou seja, olhando para a precisão de nossos cálculos de distância em comparação com os dados de entrada, não em comparação com as distâncias derivadas.

Se bem entendi sua ideia, você prefere comparar o erro absoluto com a magnitude dos dados de entrada. Usando as normas vetoriais como uma medida agregada da magnitude das entradas. Já o erro relativo padrão compara-o com a magnitude do resultado exato.

Acho que com essa métrica você tenta capturar o quanto um algoritmo está com

• Realmente não diz quantos dígitos do resultado são inexatos.
• Na verdade, a maioria dos algoritmos teria uma pontuação inferior a 1e-15. Mesmo a fórmula expandida (algoritmo baseado em pontos) teria uma pontuação limitada por algo como 5 ULP (entrada) (estimativa grosseira, não escrevi a prova completa).
• E como ambas as métricas são apenas uma versão redimensionada do erro absoluto computed - exact , elas classificariam os algoritmos na mesma ordem quando avaliados nas mesmas entradas.
  Portanto, é igual ao erro relativo usual, apenas com uma interpretação de valor menos útil (IMO).

Considere dados de entrada do tipo (1, 1e-16) vs. (1, 2e-16) . Por exemplo, se tivermos um atributo constante nos dados de entrada, digamos, um pixel branco em MNIST.
Com a equação baseada na diferença, isso vai funcionar, mas a versão de pontos tem problemas, não é? É por isso que experimentos unidimensionais podem não ser suficientes para estudar isso.

O algoritmo baseado em pontos teria um erro relativo de 1 , o que significa que o erro é tão grande quanto o resultado exato e, portanto, nenhum dígito do resultado está correto. E sua métrica teria um valor de 1e-16 o que significa que, em relação à escala da norma do vetor, apenas o 16º dígito está errado.
Não tenho certeza do que você está tentando mostrar com este exemplo.

Se ainda estamos preocupados com a precisão de euclidean_distances com float64, provavelmente é melhor resumir esta discussão em uma nova edição, pois há 100 comentários aqui.