Mismos resultados con Python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1:37a07cee5969, Dec  5 2015, 21:12:44) 
[GCC 4.2.1 (Apple Inc. build 5666) (dot 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1

Ocurre solo con distancia euclidiana y se puede reproducir usando directamente sklearn.metrics.pairwise.euclidean_distances :

import scipy
import sklearn.metrics.pairwise

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)

# compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_32], [b_32])

np.set_printoptions(precision=200)

print(dist_64_sklearn)
print(dist_32_sklearn)

No pude rastrear más el error.
Espero que esto pueda ayudar.

numpy podría usar un acumulador de mayor precisión. sí, se ve así
merece ser arreglado.

El 19 de julio de 2017 a las 12:05 a. M., "Nvauquie" [email protected] escribió:

Mismos resultados con Python 3.5:

Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1: 37a07cee5969, 5 de diciembre de 2015, 21:12:44)
[GCC 4.2.1 (compilación 5666 de Apple Inc.) (punto 3)]
NumPy 1.11.0
CIENCIA 0.18.1
Scikit-Learn 0.17.1

Ocurre solo con distancia euclidiana y se puede reproducir usando
directamente sklearn.metrics.pairwise.euclidean_distances:

importar scipy
importar sklearn.metrics.pairwise

crear vectores ayb de 64 bits que sean muy similares entre sí

a_64 = np.array ([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype = np.float64)
b_64 = np.array ([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype = np.float64)

crear versiones de 32 bits de ayb

a_32 = a_64.astype (np.float32)
b_32 = b_64.astype (np.float32)

calcular la distancia de a a b usando sklearn, tanto para 64 bits como para 32 bits

dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances ([a_32], [b_32])

np.set_printoptions (precisión = 200)

imprimir (dist_64_sklearn)
imprimir (dist_32_sklearn)

No pude rastrear más el error.
Espero que esto pueda ayudar.

-
Estás recibiendo esto porque estás suscrito a este hilo.
Responda a este correo electrónico directamente, véalo en GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-316074315 ,
o silenciar el hilo
https://github.com/notifications/unsubscribe-auth/AAEz65yy8Aq2FcsDAcWHT8qkkdXF_MfPks5sPLu_gaJpZM4OXbpZ
.

Me gustaría trabajar en esto si es posible

¡Ve a por ello!

Entonces creo que el problema radica en el hecho de que estamos usando sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y)) para calcular la distancia euclidiana
Porque si intento - (-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) obtengo la respuesta 0 para np.float32, mientras que obtengo la respuesta correcta para np.float 64.

@jnothman ¿Qué crees que debería hacer entonces? Como mencioné en mi comentario anterior, el problema probablemente sea calcular la distancia euclidiana usando sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

Entonces, ¿estás diciendo que el punto devuelve un resultado menos preciso que producto-luego-suma?

No, lo que intento decir es que el punto devuelve un resultado más preciso que el producto luego la suma.
-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) da salida [[0.]]
mientras que np.sqrt(((X-Y) * (X-Y)).sum(axis=1)) da salida [ 0.02290595]

No está claro lo que está haciendo, en parte porque no está publicando un fragmento de código completamente independiente.

Mirando rápidamente su última publicación, las dos cosas que está tratando de comparar [[0.]] y [0.022...] no tienen las mismas dimensiones (tal vez un problema de copiar y pegar, pero nuevamente es difícil saberlo porque no tener un fragmento completo).

Ok lo siento mi mal

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot

# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875,    -65.7512664794921875],  dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)

# create 32-bit versions of a and b
X = a_64.astype(np.float32)
Y = b_64.astype(np.float32)

X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]

#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
print(np.sqrt(distances))

#Euclidean distance computed using (X-Y)^2
print(np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis]))

SALIDA

[[ 0.03125]]
[[ 0.02290595136582851409912109375]]

El primer método es cómo se calcula mediante la función de distancia euclidiana.
También para aclarar lo que quise decir anteriormente fue el hecho de que suma-luego-producto tiene menor precisión incluso cuando usamos funciones numpy para hacerlo

Sí, puedo replicar esto. Veo que haciendo la resta inicialmente
permite mantener la precisión de la diferencia. Haciendo el punto
producto y luego restar (o negar y sumar), como hacemos actualmente,
pierde esta precisión ya que las cifras más significativas son mucho mayores que
las diferencias.

La implementación actual es más eficiente en memoria para un gran número de
caracteristicas. Pero supongo que la distancia euclidiana se vuelve cada vez más irrelevante
en grandes dimensiones, por lo que la memoria está dominada por el número de salida
valores.

Así que voto por adoptar la implementación numéricamente más estable durante
Implementación d-asintóticamente eficiente que tenemos actualmente. Una opinión,
@ogrisel? @agramfort?

Y esto, por supuesto, es más preocupante ya que recientemente permitimos float32s
para ser más común entre los estimadores.

Entonces, para este ejemplo, product-then-sum funciona perfectamente bien para np.float64, por lo que una posible solución podría ser convertir la entrada a float64, luego calcular el resultado y devolver el resultado convertido de nuevo a float32. Supongo que esto sería más eficiente, pero no estoy seguro de si funcionaría bien para algún otro ejemplo.

la conversión a float64 no será más eficiente en el uso de la memoria que
sustracción.

Oh, sí, lo lamentas, pero creo que usar float64 y luego hacer producto-luego-suma sería más eficiente computacionalmente, si no en memoria.

Y la razón para usar producto-luego-suma fue tener más eficiencia computacional y no eficiencia de memoria.

seguro, pero no creo que haya ninguna razón para suponer que de hecho es
más eficientes computacionalmente, excepto por no tener que realizar un
matriz intermedia. Suponiendo que limitamos la memoria de trabajo absoluta (por ejemplo, por
fragmentación), ¿por qué tomar el producto escalar, duplicar y restar normas
ser mucho más eficiente que restar y cuadrar?

¿Proporcionar puntos de referencia?

Ok, creé una secuencia de comandos de Python para comparar el tiempo necesario para restar, luego cuadrar y convertir a float64, luego producto y luego suma y resulta que si elegimos una X y una Y como vectores muy grandes, los 2 resultados son muy diferentes . También @jnothman, tenías razón, restar y luego elevar al cuadrado es más rápido.
Aquí está el guión que escribí, si hay algún problema, hágamelo saber

import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
from timeit import default_timer as timer

for i in range(9):
    X = np.random.rand(1,3 * (10**i)).astype(np.float32)
    Y = np.random.rand(1,3 * (10**i)).astype(np.float32)

    X, Y = check_pairwise_arrays(X, Y)
    XX = row_norms(X, squared=True)[:, np.newaxis]
    YY = row_norms(Y, squared=True)[np.newaxis, :]

    #Euclidean distance computed using product-then-sum
    distances = safe_sparse_dot(X, Y.T, dense_output=True)
    distances *= -2
    distances += XX
    distances += YY

    ans1 = np.sqrt(distances)

    start = timer()
    ans2 = np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis])
    end = timer()
    if ans1 != ans2:
        print(end-start)

        start = timer()
        X = X.astype(np.float64)
        Y = Y.astype(np.float64)
        X, Y = check_pairwise_arrays(X, Y)
        XX = row_norms(X, squared=True)[:, np.newaxis]
        YY = row_norms(Y, squared=True)[np.newaxis, :]
        distances = safe_sparse_dot(X, Y.T, dense_output=True)
        distances *= -2
        distances += XX
        distances += YY
        distances = np.sqrt(distances)
        end = timer()
        print(end-start)
        print('')
        if abs(ans2 - distances) > 1e-3:
            # np.set_printoptions(precision=200)
            print(ans2)
            print(np.sqrt(distances))

            print(X, Y)
            break

Vale la pena probar cómo se escala con el número de muestras, no solo con el
número de características ... tomar normas puede tener el beneficio de calcular algunas
cosas una vez por muestra, no una vez por par de muestras

El 20 de octubre de 2017 a las 2:39 a. M., "Osaid Rehman Nasir" [email protected]
escribió:

Ok, creé un script de Python para comparar el tiempo que tomó
resta-luego-cuadrado y conversión a float64 luego producto-luego-suma
y resulta que si elegimos X e Y como vectores muy grandes, entonces los 2
los resultados son muy diferentes. También @jnothman https://github.com/jnothman
tenías razón, restar y luego elevar al cuadrado es más rápido.
Aquí está el guión que escribí, si hay algún problema, hágamelo saber

importar numpy como np
importar scipy
de sklearn.metrics.pairwise importar check_pairwise_arrays, row_norms
de sklearn.utils.extmath importar safe_sparse_dot
desde timeit importar default_timer como temporizador

para i en el rango (9):
X = np.random.rand (1,3 * (10 i)). Astype (np.float32)Y = np.random.rand (1,3 * (10 i)). Astype (np.float32)

X, Y = check_pairwise_arrays (X, Y)
XX = row_norms (X, squared = True) [:, np.newaxis]
YY = row_norms (Y, squared = True) [np.newaxis,:]

#Distancia euclidiana calculada utilizando producto-luego-suma
distancias = safe_sparse_dot (X, YT, dense_output = True)
distancias * = -2
distancias + = XX
distancias + = YY

ans1 = np.sqrt (distancias)

inicio = temporizador ()
ans2 = np.sqrt (row_norms (XY, squared = True) [:, np.newaxis])
fin = temporizador ()
si ans1! = ans2:
imprimir (fin-inicio)

  start = timer()
  X = X.astype(np.float64)
  Y = Y.astype(np.float64)
  X, Y = check_pairwise_arrays(X, Y)
  XX = row_norms(X, squared=True)[:, np.newaxis]
  YY = row_norms(Y, squared=True)[np.newaxis, :]
  distances = safe_sparse_dot(X, Y.T, dense_output=True)
  distances *= -2
  distances += XX
  distances += YY
  distances = np.sqrt(distances)
  end = timer()
  print(end-start)
  print('')
  if abs(ans2 - distances) > 1e-3:
      # np.set_printoptions(precision=200)
      print(ans2)
      print(np.sqrt(distances))

      print(X, Y)
      break

-
Estás recibiendo esto porque te mencionaron.
Responda a este correo electrónico directamente, véalo en GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-337948154 ,
o silenciar el hilo
https://github.com/notifications/unsubscribe-auth/AAEz6z5o2Ao_7V5-Lflb4HosMrHCeOrVks5st209gaJpZM4OXbpZ
.

de todos modos, ¿te gustaría enviar un PR, @ragnerok?

si claro, que quieres que haga?

proporcionar una implementación más estable, también una prueba que fallaría bajo el
implementación actual, e idealmente un punto de referencia que muestre que no perdemos
mucho del cambio, en casos razonables.

Quería preguntar si es posible encontrar la distancia entre cada par de filas con vectorización. No puedo pensar en cómo hacerlo vectorizado.

¿Te refieres a la diferencia (no a la distancia) entre pares de filas? Seguro que puedes hacerlo si estás trabajando con matrices numpy. Si tiene matrices con formas (n_samples1, n_features) y (n_samples2, n_features), solo necesita remodelarlas a (n_samples1, 1, n_features) y (1, n_samples2, n_features) y hacer la resta:

>>> X = np.random.randint(10, size=(10, 5))
>>> Y = np.random.randint(10, size=(11, 5))
X.reshape(-1, 1, X.shape[1]) - Y.reshape(1, -1, X.shape[1])

Sí, gracias, eso realmente ayudó 😄

También quería preguntar si proporciono una implementación más estable. No usaré X_norm_squared y Y_norm_squared. Entonces, ¿los elimino también de los argumentos o debo advertir que no es de ninguna utilidad?

Creo que quedarán obsoletos, pero es posible que primero necesitemos estar seguros de que
no hay ningún caso en el que debamos mantener esa versión.

vamos a tener mucho cuidado al cambiar esto. es un ampliamente utilizado y
implementación de larga data. debemos asegurarnos de no ralentizar ninguna
casos. es posible que debamos hacer la operación en fragmentos para evitar un alto nivel de memoria
uso (que quizás sea más complicado por el hecho de que esto se llama
dentro de las funciones que se fragmentan para minimizar el retiro de la memoria de salida de
distancias por pares).

Realmente me gustaría escuchar a otros desarrolladores centrales que sepan sobre computacional
costes y precisión numérica ... @ogrisel , @lesteve , @rth ...

El 5 de noviembre de 2017 a las 5:27 a. M., "Osaid Rehman Nasir" [email protected]
escribió:

También quería preguntar si proporciono una implementación más estable.
utilizando X_norm_squared e Y_norm_squared. Entonces, los elimino del
argumentos también o debo advertir que no sirve de nada?

-
Estás recibiendo esto porque te mencionaron.
Responda a este correo electrónico directamente, véalo en GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-341919282 ,
o silenciar el hilo
https://github.com/notifications/unsubscribe-auth/AAEz63izdpQGDEuW32m8Aob6rrsvV6q-ks5szKyHgaJpZM4OXbpZ
.

pero sería más fácil discutir con precisión si abre un PR

Ok, abriré un PR entonces, con una implementación muy básica de esta función

La pregunta es qué se debe hacer al respecto para la versión 0.20. ¿Podría haber algunas mejoras simples / temporales (evento a costa, por ejemplo, del uso de memoria) que podrían considerarse?

La solución y el análisis propuestos en el n. ° 11271 son definitivamente muy valiosos, pero podría requerir más discusión para asegurarse de que esta sea la solución óptima. En particular, me preocupa el hecho de que ahora tenemos una discusión pendiente sobre la memoria de trabajo global óptima en https://github.com/scikit-learn/scikit-learn/issues/11506 dependiendo del tipo de CPU, etc. agregaría otro nivel de fragmentación y la complejidad del conjunto sería obtener un poco de control en mi opinión. Pero tal vez sea solo yo, buscando una segunda opinión.

¿Qué crees que se debería hacer sobre este tema para el lanzamiento @jnothman @amueller @ogrisel ?

La estabilidad triunfa sobre la eficiencia. Los problemas de estabilidad deben solucionarse incluso cuando
la eficiencia aún necesita ajustes.

El enfoque de working_memory era hacer cosas como silueta con una muestra grande
los tamaños funcionan. También mejoró la eficiencia, pero eso se puede ajustar en el
línea.

Creo firmemente que deberíamos intentar arreglar las distancias_euclidianas con
float32 in. Lo dividimos en 0.19 asumiendo que podíamos hacer
euclidean_distances funciona en 32 bits de una manera ingenua.

Estoy de acuerdo en que necesitamos una solución. Mi preocupación aquí no es la eficiencia sino la complejidad agregada en la base del código.

Dando un paso atrás, la implementación euclidiana de scipy parece ser de 10 líneas de código C y para 32 bits, simplemente conviértalas en 64 bits. Entiendo que no es el más rápido, pero conceptualmente es fácil de seguir y comprender. En scikit-learn, usamos el truco para hacer cálculos más rápidos en BLAS, luego hay posibles mejoras debido en https://github.com/scikit-learn/scikit-learn/pull/10212 y ahora la posible solución fragmentada para euclidiana distancia en 32 bits.

Solo estoy buscando información sobre cuál debería ser la dirección general sobre este tema (por ejemplo, intente subir algo a scipy, etc.).

scipy no parece preocupado por copiar los datos ...

Muévase a 0.21 siguiendo el PR.

¿Quitar el bloqueador?

sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))

es numéricamente inestable, si el punto (x, x) y el punto (y, y) tienen una magnitud similar a la del punto (x, y) debido a lo que se conoce como cancelación catastrófica .

Esto no solo afecta la precisión del FP32, sino que, por supuesto, es más prominente y fallará mucho antes.

Aquí hay un caso de prueba simple que muestra cuán malo es esto incluso con doble precisión:

import numpy
from sklearn.metrics.pairwise import euclidean_distances

a = numpy.array([[100000001, 100000000]])
b = numpy.array([[100000000, 100000001]])

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

a = numpy.array([[10001, 10000]], numpy.float32)
b = numpy.array([[10000, 10001]], numpy.float32)

print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))

sklearn calcula una distancia de 0 aquí en ambas ocasiones, en lugar de sqrt (2).

Aquí se puede encontrar una discusión de los problemas numéricos de la varianza y la covarianza, y esto trivialmente se traslada a este enfoque de aceleración de la distancia euclidiana:

Erich Schubert y Michael Gertz.
Cálculo paralelo numéricamente estable de (Co-) varianza.
En: Actas de la 30ª Conferencia internacional sobre gestión de bases de datos científicas y estadísticas (SSDBM), Bolzano-Bozen, Italia. 2018, 10: 1–10: 12

En realidad, la coordenada y se puede eliminar de ese caso de prueba, la distancia correcta se convierte trivialmente en 1. Hice una solicitud de extracción que desencadena este problema numérico:

    XA = np.array([[10000]], np.float32)
    XB = np.array([[10001]], np.float32)
    assert_equal(euclidean_distances(XA, XB)[0,0], 1)

No creo que mi artículo mencionado anteriormente proporcione una solución para este problema; simplemente calcule la distancia euclidiana como sqrt (sum (power ())) y es de un solo paso y tiene una precisión razonable. La pérdida ya está en usar los cuadrados, es decir, el punto (x, x) ya está perdiendo la precisión.

@amueller ya que el problema puede ser más grave de lo esperado, sugiero volver a agregar la etiqueta del bloqueador ...

Gracias por este sencillo ejemplo.

La razón por la que se implementa de esta manera es porque es mucho más rápido. Vea abajo:

x = np.random.random_sample((1000, 1000))

%timeit euclidean_distances(x,x)
20.6 ms ± 452 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit cdist(x,x)
695 ms ± 4.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Aunque el número de operaciones es del mismo orden en ambos métodos (1,5 veces más en el segundo), la aceleración proviene de la posibilidad de utilizar bibliotecas BLAS bien optimizadas para la multiplicación de matrices.

Esto sería una gran desaceleración para varios estimadores en scikit-learn.

Sí, pero sólo 3-4 dígitos de precisión con FP32, y 7-8 dígitos con FP64 causa una imprecisión importante, ¿verdad? En particular, dado que tales errores tienden a amplificarse ...

Bueno, no estoy diciendo que esté bien ahora. :)
Estoy diciendo que tenemos que encontrar una solución intermedia.
Hay un PR (# 11271) que propone lanzar en float64 para hacer los cálculos. In no soluciona el problema de float64 pero proporciona una mejor precisión para float32.

¿Tiene un ejemplo en el que el uso de un estimador que usa euclidean_distances da resultados incorrectos debido a la pérdida de precisión?

Ciertamente, sigo pensando que esto es un gran problema y debería ser un bloqueador de 0.21. Fue un problema introducido para 32 bits en 0.19, y no es un buen estado de cosas dejarlo. Ojalá lo hubiéramos resuelto antes en 0.20, y estaría bien, o incluso con ganas, de ver # 11271 fusionado en el ínterin. Los únicos problemas en ese PR que conozco son la optimización envolvente de la eficiencia de la memoria, que es un profundo agujero de conejo.

Hemos tenido esta versión "rápida" durante mucho tiempo, pero siempre en float64. Sé, @ kno10 , que tiene problemas con la precisión. ¿Tiene una heurística buena y rápida para que averigüemos cuándo podría ser un problema y usemos una solución más lenta pero más segura?

Sí, pero solo 3-4 dígitos de precisión con FP32 y 7-8 dígitos con FP64 causan una imprecisión sustancial, ¿no?

¡Gracias por ilustrar este problema con un ejemplo muy simple!

Sin embargo, no creo que el problema esté tan extendido como usted sugiere; afecta principalmente a muestras cuya distancia mutua es pequeña con respecto a sus normas.

La siguiente figura ilustra esto, para 2e6 pares de muestras aleatorias, donde cada muestra 1D está en el intervalo [-100, 100]. El error relativo entre la implementación de scikit-learn y scipy se grafica en función de la distancia entre las muestras, normalizada por sus normas L2, es decir,

d_norm(A, B) = d(A, B) / sqrt(‖A‖₂*‖B‖₂)

(no estoy seguro de que sea la parametrización correcta, pero solo para obtener resultados algo invariantes a la escala de datos),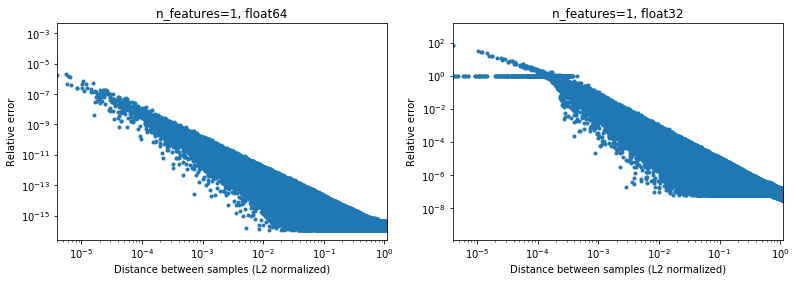

Por ejemplo,

1. si se toma [10000] y [10001] la distancia normalizada L2 es 1e-4 y el error relativo en el cálculo de la distancia será 1e-8 en 64 bits y> 1 en 32 bits (O 1e -8 y> 1 en valor absoluto respectivamente). En 32 bits, este caso es bastante terrible.
2. por otro lado, para [1] y [10001] , el error relativo será ~ 1e-7 en 32 bits, o la máxima precisión posible.

La pregunta es con qué frecuencia ocurrirá el caso en la práctica en aplicaciones de AA.

Curiosamente, si pasamos a 2D, nuevamente con una distribución aleatoria uniforme, será difícil encontrar puntos que estén muy cerca,

Por supuesto, en realidad, nuestros datos no serán muestreados uniformemente, pero para cualquier distribución debido a la maldición de la dimensionalidad, la distancia entre dos puntos cualesquiera convergerá lentamente a valores muy similares (diferentes de 0) a medida que aumenta la dimensionalidad. Si bien es un problema de ML general, aquí puede mitigar un poco este problema de precisión, incluso para una dimensionalidad relativamente baja. Debajo de los resultados de n_features=5 ,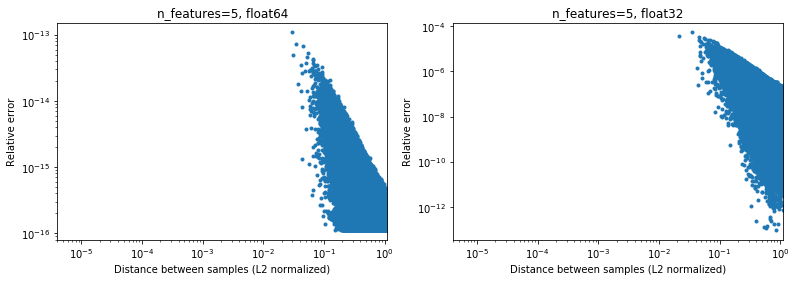
.

Entonces, para los datos centrados, al menos en 64 bits, puede que no sea un gran problema en la práctica (asumiendo que hay más de 2 características). La aceleración computacional de 50x (como se ilustra arriba) puede valer la pena (en 64 bits). Por supuesto, siempre se puede agregar 1e6 a algunos datos normalizados en [-1, 1] y decir que los resultados no son precisos, pero yo diría que lo mismo se aplica a una serie de algoritmos numéricos y al trabajar con datos expresados ​​en el sexto dígito significativo solo busca problemas.

(El código de las figuras anteriores se puede encontrar aquí ).

Cualquier enfoque rápido que use la versión de punto (x, x) + punto (y, y) -2 Creo que necesitará duplicar la precisión de los productos punto para llegar a aprox. entrada (y supongo que si un usuario proporciona datos float32, entonces querrán precisión float32, con float64, querrán precisión float64). Es posible que pueda hacer esto con algunos trucos (piense en la suma de Kahan), pero es muy probable que le cueste mucho más de lo que ganó en primer lugar.

No puedo decir cuántos gastos generales se obtienen al convertir float32 en float64 sobre la marcha para usar este enfoque. Al menos para float32, a mi entender, hacer todos los cálculos y almacenar los productos punto como float64 debería estar bien.

En mi humilde opinión, las ganancias de rendimiento (que no son exponenciales, solo un factor constante) no valen la pena la pérdida de precisión (que puede morderlo inesperadamente) y la forma correcta es no usar este truco problemático. Sin embargo, puede ser posible optimizar aún más el código haciendo el cálculo "tradicional", por ejemplo, para usar AVX. Porque sum ((xy) * 2) es casi difícil de implementar en AVX.Como mínimo, sugeriría cambiar el nombre del método a approximate_euclidean_distances , debido a la precisión a veces baja (que empeora cuanto más se acercan los dos valores, que * puede estar bien inicialmente y luego comenzar a importar cuando converge a un valor óptimo) , para que los usuarios estén al tanto de este problema.

@rth gracias por las ilustraciones. Pero, ¿qué pasa si está tratando de optimizar, por ejemplo, x hacia un valor óptimo? Lo más probable es que el óptimo no sea cero (si siempre fuera su centro de datos, la vida sería excelente) y, eventualmente, los deltas que está calculando para gradientes, etc.pueden tener algunas diferencias muy pequeñas.
De manera similar, en la agrupación, no todos los grupos tendrán sus centros cerca de cero, pero en particular con muchos grupos, es muy posible que x ≈ centro con unos pocos dígitos.

Sin embargo, en general, estoy de acuerdo en que este problema debe solucionarse. En cualquier caso, necesitamos documentar los problemas de precisión de la implementación actual lo antes posible.

En general, aunque no creo que esta discusión deba ocurrir en scikit-learn. La distancia euclidiana se utiliza en varios campos de la informática científica y la lista de correo scipy de la OMI o problemas es un lugar mejor para discutirlo: esa comunidad también tiene más experiencia con tales problemas de precisión numérica. De hecho, lo que tenemos aquí es un algoritmo rápido pero algo aproximado. Es posible que tengamos que implementar algunas soluciones alternativas a corto plazo, pero a largo plazo sería bueno saber que esto contribuirá allí.

Para 32 bits, https://github.com/scikit-learn/scikit-learn/pull/11271 puede ser una solución, simplemente no estoy tan interesado en múltiples niveles de fragmentación en toda la biblioteca, ya que eso aumenta la complejidad del código y quiero asegurarse de que no haya una mejor manera de evitarlo.

¡Gracias por tu respuesta @ kno10! (Mis comentarios anteriores aún no lo tienen en cuenta) Responderé un poco más tarde.

Sí, la convergencia a algún punto fuera del origen puede ser un problema.

En mi humilde opinión, las ganancias de rendimiento (que no son exponenciales, solo un factor constante) no valen la pena la pérdida de precisión (que puede morderlo inesperadamente) y la forma correcta es no usar este truco problemático.

Bueno, una ralentización> 10x para su cálculo en 64 bits tendrá un efecto muy real en los usuarios.

Sin embargo, puede ser posible optimizar aún más el código haciendo el cálculo "tradicional", por ejemplo, para usar AVX. Porque sum ((xy) ** 2) es casi difícil de implementar en AVX.

Probé una implementación ingenua rápida con numba (que debería usar SSE),

@numba.jit(nopython=True, fastmath=True)              
def pairwise_distance_naive(A, B):
    n_samples_a, n_features_a = A.shape
    n_samples_b, n_features_b = B.shape
    assert n_features_a == n_features_b
    distance = np.empty((n_samples_a, n_samples_b), dtype=A.dtype)
    for i in range(n_samples_a):
        for j in range(n_samples_b):
            psum = 0.0
            for k in range(n_features_a):
                psum += (A[i, k] - B[j, k])**2
            distance[i, j] = math.sqrt(psum)
    return distance

obteniendo una velocidad similar a scipy cdist hasta ahora (pero no soy un experto en numba), y tampoco estoy seguro del efecto de fastmath .

usando la versión dot (x, x) + dot (y, y) -2 * dot (x, y)

Solo para referencia futura, lo que estamos haciendo actualmente es aproximadamente lo siguiente (porque hay una dimensión que no se muestra en la notación anterior),

def quadratic_pairwise_distance(A, B):
    A2 = np.einsum('ij,ij->i', A, A)
    B2 = np.einsum('ij,ij->i', B, B)
    return np.sqrt(A2[:, None] + B2[None, :] - 2*np.dot(A, B.T))

donde tanto einsum como dot ahora usan BLAS. Me pregunto si, además de usar BLAS, esto también hace la misma cantidad de operaciones matemáticas que la primera versión anterior.

Me pregunto si, además de usar BLAS, esto también hace la misma cantidad de operaciones matemáticas que la primera versión anterior.

No. El ((x - y) * 2.sum ()) realiza* n_samples_x * n_samples_y * n_features * (1 resta + 1 suma + 1 multiplicación)
mientras que xx + yy -2x.y realiza
n_samples_x * n_samples_y * n_features * (1 suma + 1 multiplicación) .
Hay una relación de 2/3 para el número de operaciones entre las 2 versiones.

Siguiendo la discusión anterior,

• Hizo un PR para permitir opcionalmente calcular distancias euclidianas exactamente https://github.com/scikit-learn/scikit-learn/pull/12136
• Algunos WIP para ver si podemos detectar y mitigar los puntos problemáticos en https://github.com/scikit-learn/scikit-learn/pull/12142

Para 32 bits, todavía necesitamos fusionar https://github.com/scikit-learn/scikit-learn/pull/11271 de alguna forma aunque, en mi opinión, los PR anteriores son algo ortogonales.

FYI: al solucionar algunos problemas en OPTICS y actualizar la prueba para usar los resultados de referencia de ELKI, estos fallan con metric="euclidean" pero tienen éxito con metric="minkowski" . Las diferencias numéricas son lo suficientemente grandes como para causar un orden de procesamiento diferente (simplemente disminuir el umbral no es suficiente).

https://github.com/kno10/scikit-learn/blob/ab544709a392e4dc7b22e9fd60c4755baf3d3053/sklearn/cluster/tests/test_optics.py#L588

Realmente no estoy al tanto de esto, pero me sorprende que no haya una solución existente. Este parece ser un cálculo muy común y parece que estamos reinventando la rueda. ¿Alguien ha intentado llegar a la comunidad científica informática más amplia?

Todavía no, pero estoy de acuerdo en que deberíamos. Lo único que encontré sobre esto en scipy fue https://github.com/scipy/scipy/pull/2815 y problemas vinculados.

Siento que @jeremiedbb podría tener una idea.

Desafortunadamente, todavía no es satisfactorio :(

Nos gustaría confiar en una biblioteca altamente optimizada para este tipo de cálculo, como hacemos para el álgebra lineal con bibliotecas BLAS como OpenBLAS o MKL. Pero la distancia euclidiana no forma parte de ella. El truco de los puntos es un intento de hacerlo confiando en la subrutina de multiplicación matriz-matriz de nivel 3 de BLAS. Pero esto no es preciso y no hay forma de hacerlo más preciso utilizando el mismo método. Tenemos que reducir nuestra expectativa en términos de velocidad o en términos de precisión.

Creo que en algunas situaciones, la precisión total no es obligatoria y mantener el método rápido está bien. Aquí es cuando las distancias se utilizan para "encontrar las tareas más cercanas". Los problemas de precisión en el método rápido aparecen cuando las distancias entre puntos son pequeñas en comparación con su norma (en una proporción ~ <1e-4 para float 32 y ~ <1e-8 para float64). Primero, para que ocurra esta situación, el conjunto de datos debe ser bastante denso. Luego, para tener un error de pedido, debe tener los dos puntos más cercanos dentro de casi la misma distancia. Además, en ese caso, desde el punto de vista del LD, ambos conducirían a ajustes casi igualmente buenos.

En la situación anterior, hay algo que podemos hacer para reducir la frecuencia de estos ordenamientos incorrectos (¿hasta 0?). En la situación argmin de distancia por pares. Podemos mover el desorden a puntos que no son los más cercanos. Esencialmente usando el hecho de que una de las normas no es necesaria para encontrar el argmin, ver comentario . Tiene 2 ventajas. Es más robusto (hasta ahora no he encontrado un pedido incorrecto) y es aún más rápido porque evita algunos cálculos.

Un inconveniente, aún en la misma situación, si al final queremos las distancias reales a los puntos más cercanos, las distancias calculadas con el método anterior no se pueden utilizar. Solo se calculan parcialmente y de todos modos no son precisos. Necesitamos volver a calcular las distancias desde cada punto hasta su punto más cercano. Pero esto es rápido porque para cada punto solo hay una distancia para calcular.

Me pregunto que lo que describí anteriormente cubre todos los casos de uso de euclidean_distances en sklearn. Pero sugiero hacerlo donde sea que se pueda aplicar. Para hacer eso, podemos agregar un nuevo parámetro a euclidean_distances para calcular solo la parte necesaria para encadenarlo con argmin. Luego úselo en pairwise_distances_argmin y en pairwise_distances_argmin_min (vuelva a calcular las distancias mínimas reales al final en este último).

Cuando no podamos hacer eso, recurra al lento pero preciso, o agregue un interruptor como en # 12136.
Podemos intentar optimizarlo un poco para reducir la caída del rendimiento porque estoy de acuerdo en que esto no parece óptimo. Tengo algunas ideas para eso.

Otra posibilidad para seguir usando BLAS es combinar axpy con nrm2 pero esto está lejos de ser óptimo. Ambas son funciones BLAS de nivel 1 e implica una copia. Esto solo sería más rápido en una dimensión> 100.
Lo ideal sería que la distancia euclidiana se incluyera en BLAS ...

Finalmente, existe otra solución, consistente en upcasting. Esto se hace en # 11271 para float32. La ventaja es que la velocidad es solo la mitad de la actual y se mantiene la precisión. Sin embargo, no resuelve el problema de float64. Tal vez podamos encontrar una manera de hacer algo similar en cython para float64. No sé exactamente cómo, pero usando 2 números float64 para simular un float128. Puedo intentarlo para ver si es algo factible.

Lo ideal sería que la distancia euclidiana se incluyera en BLAS ...

¿Es eso algo que las bibliotecas considerarían? Si OpenBLAS lo hace, ya estaríamos en una situación bastante buena ...

Además, ¿cuáles son las diferencias exactas entre nosotros haciéndolo y el BLAS haciéndolo? ¿Detectar las capacidades de la CPU y decidir qué implementación usar, o algo así? ¿O simplemente habiendo compilado versiones para arquitecturas más diversas?
¿O simplemente gasta más tiempo / energía escribiendo implementaciones eficientes?

Esto es interesante: una implementación alternativa del método rápido inestable pero que afirma ser mucho más rápido que sklearn:
https://github.com/droyed/eucl_dist
(no resuelve este problema en absoluto, aunque lol)

Esta discusión parece relacionada https://github.com/scipy/scipy/issues/5657

Esto es lo que hace julia: https://github.com/JuliaStats/Distances.jl/blob/master/README.md#precision -for-euclidean-and-sqeuclidean
Permite establecer un umbral de precisión para forzar el recálculo.

Respondiendo a mi propia pregunta: OpenBLAS tiene lo que parece un ensamblaje escrito a mano para cada procesador (¡no arquitectura!) Y heutísticas para elegir kernels para diferentes tamaños de problemas. Así que no creo que se trate tanto de introducirlo en openblas como de encontrar a alguien que escriba / optimice todos esos kernels ...

¡Gracias por los pensamientos adicionales!

En una respuesta parcial,

Nos gustaría confiar en una biblioteca altamente optimizada para este tipo de cálculo, como hacemos para el álgebra lineal con bibliotecas BLAS como OpenBLAS o MKL.

Sí, también esperaba que pudiéramos hacer más de esto en BLAS. La última vez que no miré nada en la API BLAS estándar se ve lo suficientemente cerca (pero no soy un experto en eso). BLIS puede ofrecer más flexibilidad, pero dado que no lo usamos de forma predeterminada, tiene un uso algo limitado (aunque numpy podría algún día https://github.com/numpy/numpy/issues/7372)

Esto es lo que hace julia: permite establecer un umbral de precisión para forzar el recálculo.

¡Genial saber!

¿Deberíamos abrir un problema separado para el cálculo aproximado más rápido vinculado anteriormente? Parece interesante

Su aceleración en la CPU de x2-x4 podría deberse a https://github.com/scikit-learn/scikit-learn/pull/10212 .

Preferiría abrir un problema en scipy una vez que hayamos estudiado esta pregunta lo suficiente como para encontrar una solución razonable allí (y luego posiblemente respaldarla) ya que creo que la distancia euclidiana es algo lo suficientemente básico que debería ser de interés para muchas personas fuera de ML. (y al mismo tiempo, sería útil tener la opinión de la gente, por ejemplo, sobre cuestiones de precisión).

Es hasta 60x, ¿verdad?

Esto es interesante: una implementación alternativa del método rápido inestable pero que afirma ser mucho más rápido que sklearn

tarareo no estoy seguro de eso. Están comparando %timeit pairwise_distances(a,b, 'sqeuclidean') , que usa el de scipy. Deberían hacer %timeit pairwise_distances(a,b, 'euclidean', metric_params={'squared': True}) y su aceleración no sería tan buena :)
Como se mostró mucho antes en la discusión, sklearn puede ser 35 veces más rápido que scipy

Sí, los puntos de referencia son solo ~ 30% mejores con metric="euclidean" (en lugar de squeclidean ),

In [1]: from eucl_dist.cpu_dist import dist                                                                                                                  
    ... import numpy as np                                                                                                                                   
In [4]: rng = np.random.RandomState(1)                                                                                                                        
    ... a = rng.rand(1000, 300)                                                                                                                              
    ...b = rng.rand(1000, 300)                                                                                                                              

In [7]: from sklearn.metrics.pairwise import pairwise_distances                                                                                              
In [8]: %timeit pairwise_distances(a, b, 'sqeuclidean')                                                                                                      
214 ms ± 2.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [9]: %timeit pairwise_distances(a, b)                                                                                                                     
27.4 ms ± 2.48 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [10]: from eucl_dist.cpu_dist import dist                                                                                                                 
In [11]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float32')                                                                                
20.8 ms ± 330 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [12]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float64')                                                                                
20.4 ms ± 222 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

¿Es eso algo que las bibliotecas considerarían? Si OpenBLAS lo hace, ya estaríamos en una situación bastante buena ...

No suena sencillo. BLAS es un conjunto de especificaciones para rutinas de álgebra lineal y hay varias implementaciones del mismo. No sé qué tan abiertos están a agregar nuevas funciones que no estén en las especificaciones originales. Para eso, tal vez blis sería más abierto, pero como se dijo antes, no es el predeterminado por ahora.

Abrió https://github.com/scikit-learn/scikit-learn/issues/12600 en el manejo de sqeuclidean vs euclidean en pairwise_distances .

Necesito algo de claridad sobre lo que queremos para esto. ¿Queremos que pairwise_distances esté cerca - en el sentido de all_close - tanto para 'euclidiana' como para 'sqeuclidiana'?

Es un poco complicado. El hecho de que x esté cerca de y no significa que x² esté cerca de y². La precisión se pierde durante la cuadratura.

La solución de julia vinculada anteriormente es muy interesante y es bastante sencilla de implementar. Sin embargo, sospecho que no funciona como se esperaba para 'sqeuclidean'. Sospecho que debe establecer el umbral muy por debajo para obtener la precisión deseada.

El problema de establecer un umbral muy bajo es que induce muchos recálculos y una gran caída en el rendimiento. Sin embargo, esto se ve mitigado por la dimensión del conjunto de datos. El mismo umbral activará muchos menos recálculos en grandes dimensiones (las distancias son mayores).

Tal vez podamos tener 2 implementaciones y cambiar según la dimensión del conjunto de datos. El lento pero seguro para los de baja dimensión (no hay mucha diferencia entre scipy y sklearn en ese caso de todos modos) y el rápido + umbral para los de alta dimensión.

Esto necesitará algunos puntos de referencia para encontrar cuándo cambiar y establecer el umbral, pero esto puede ser un rayo de esperanza :)

Aquí hay algunos puntos de referencia para la comparación de velocidades entre scipy y sklearn. Los puntos de referencia comparan sklearn.metrics.pairwise.euclidean_distances(X,X) con scipy.spatial.distance.cdist(X,X) para X de todos los tamaños. El número de muestras va de 2⁴ (16) a 2¹³ (8192), y el número de características va de 2⁰ (1) a 2¹³ (8192).

El valor en cada celda es la aceleración de sklearn vs scipy, es decir, por debajo de 1 sklearn es más lento y por encima de 1 sklearn es más rápido.

El primer punto de referencia está utilizando la implementación MKL de BLAS y un solo núcleo.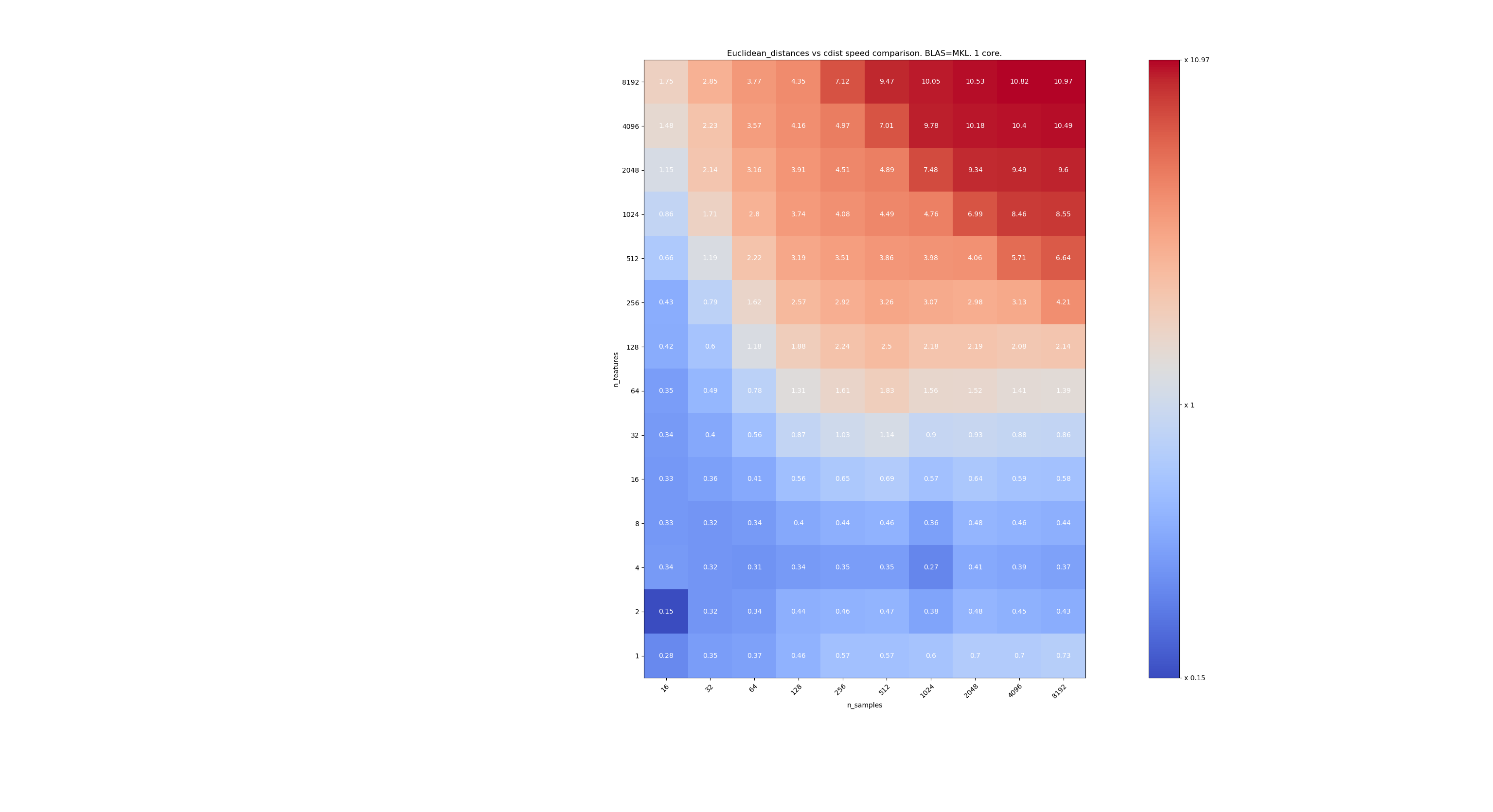

El segundo está utilizando la implementación OpenBLAS de BLAS y un solo núcleo. Es solo para comprobar que tanto MKL como OpenBLAS tienen el mismo comportamiento.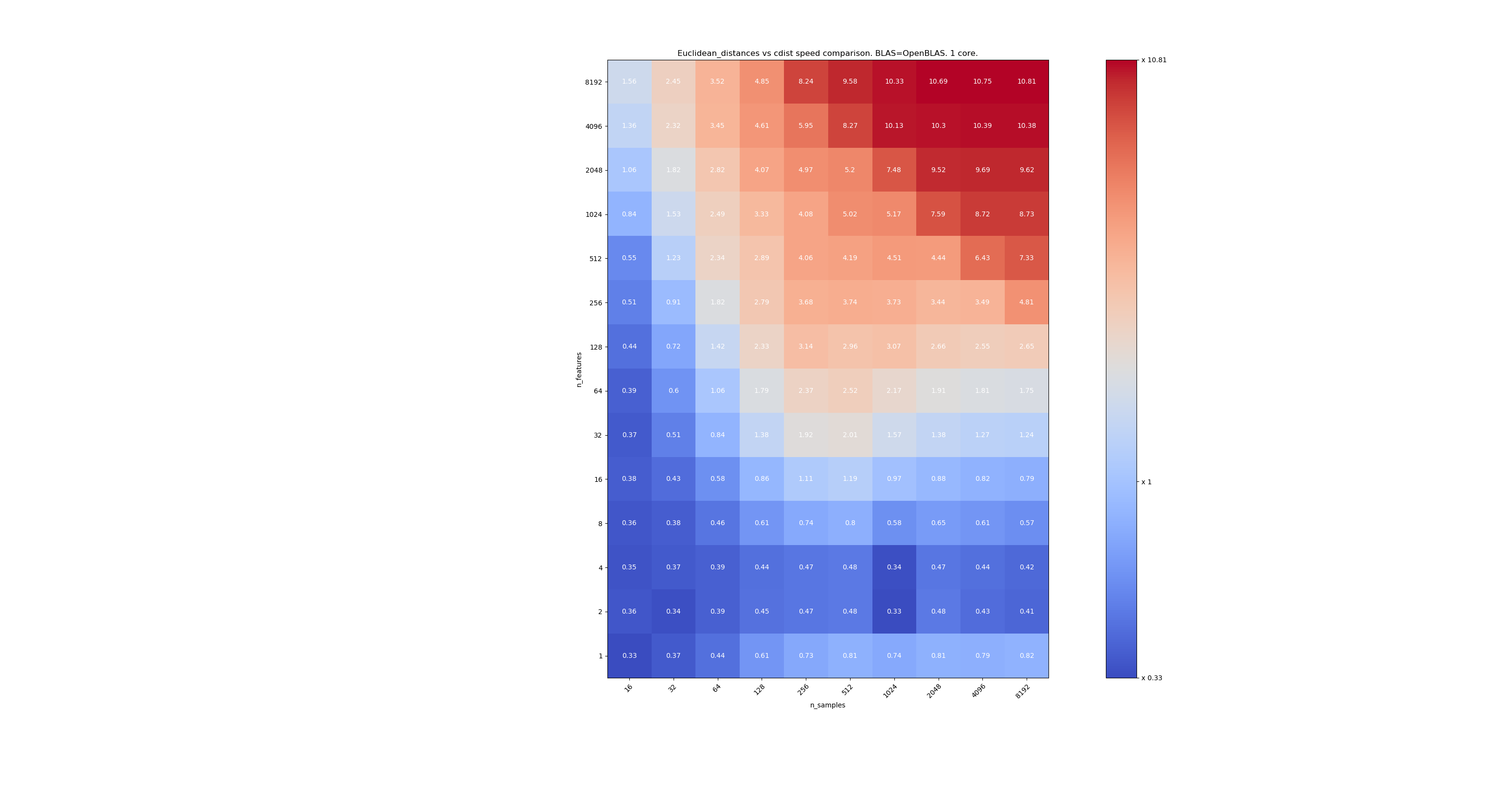

El tercero está utilizando la implementación MKL de BLAS y 4 núcleos. La cuestión es que euclidean_distances se paraleliza a través de una función BLAS LEVEL 3 pero cdist solo usa una función BLAS LEVEL 1. Curiosamente, casi no cambia la frontera.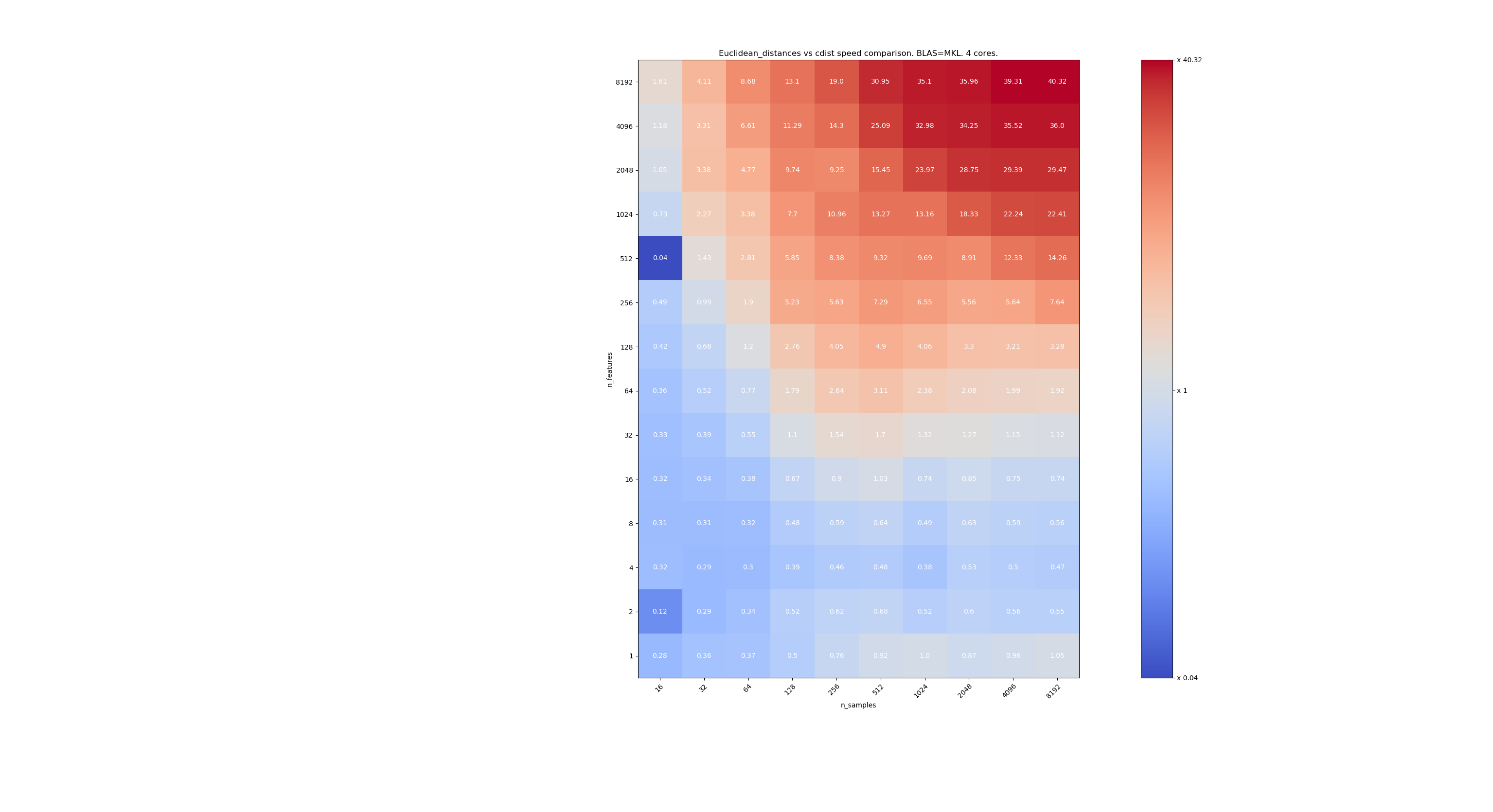

Cuando n_samples no es demasiado bajo (> 100), parece que la frontera está alrededor de 32 características. Podríamos decidir usar cdist cuando n_features <32 y euclidean_distances cuando n_features> 32. Esto es más rápido y no hay problemas de precisión. Esto también tiene la ventaja de que cuando n_features es pequeño, el umbral de julia conduce a muchos recálculos. Usar cdist evita eso.

Cuando n_features> 32, podemos mantener la implementación euclidean_distances , actualizada con el umbral de julia. Agregar el umbral no debería ralentizar demasiado euclidean_distances porque la cantidad de características es lo suficientemente alta como para que solo sean necesarios unos pocos cálculos.

@jeremiedbb genial, gracias por el análisis. La conclusión me parece un gran camino a seguir.

Oh, supongo que todo esto fue por float64, ¿verdad? ¿Qué hacemos con float32? upcast siempre? upcast para> 32 funciones?

No he leído los comentarios detenidamente (lo haré pronto), solo para su información, float64 tiene limitaciones, vea # 12128

@ qinhanmin2014 sí, la precisión de float64 tiene limitaciones, pero es lo suficientemente precisa para producir resultados fp32 confiables por lo que puedo decir. La pregunta es en qué parámetros un upcast a fp64 es realmente más barato que usar cdist de scipy.
Como se vio en los puntos de referencia anteriores, incluso BLAS multinúcleo generalmente no es más rápido. Esto parece ser mayormente válido para datos de alta dimensión (más de 64 dimensiones; antes de eso, el beneficio generalmente no vale la pena el esfuerzo en mi humilde opinión), y dado que las distancias euclidianas no son tan confiables en datos densos de alta dimensión, ese caso de uso en mi humilde opinión no es de mayor importancia. . Muchos usuarios tendrán menos de 10 dimensiones. En estos casos, ¿cdist suele ser más rápido?

Oh, supongo que todo esto fue por float64, ¿verdad?

En realidad, es para float32 y float64 (me refiero a muy similar). Sugiero usar siempre cdist cuando n_features <32.

La pregunta es en qué parámetros un upcast a fp64 es realmente más barato que usar cdist de scipy.

La conversión ascendente se ralentizará en un factor de ~ 2, así que supongo que alrededor de n_features = 64.

Muchos usuarios tendrán menos de 10 dimensiones.

Pero no todo el mundo, por lo que aún necesitamos encontrar una solución para datos de alta dimensión.

Muy buen análisis @jeremiedbb !

Para datos de baja dimensión, definitivamente tendría sentido usar cdist.

Además, el cdist de FYI scipy actualiza float32 a float64 https://github.com/scipy/scipy/issues/8771#issuecomment -384015674, no estoy seguro de si esto se debe a problemas de precisión o algo más.

En general, creo que podría tener sentido agregar el parámetro "algoritmo" a euclidean_distance como se sugiere en https://github.com/scikit-learn/scikit-learn/pull/12601#pullrequestreview -176076355, posiblemente con un valor predeterminado de "Ninguno" para que también se pueda configurar a través de una opción global como en https://github.com/scikit-learn/scikit-learn/pull/12136.

También hay un enfoque interesante en Eigen3 para calcular normas estables: https://eigen.tuxfamily.org/dox/StableNorm_8h_source.html (que todavía no he asimilado realmente)

Buena explicación, mejoró mi comprensión.

No hemos progresado en esto en el sprint y probablemente deberíamos ... y @rth no está hoy.

Puedo unirme de forma remota si estableces una hora. ¿Quizás al comienzo de la tarde?

Para resumir la situación,

Para cuestiones de precisión en los cálculos de distancia euclidiana,

• en el caso de baja dimensión, como @jeremiedbb mostró arriba, probablemente deberíamos usar cdist
• en el caso de alta dimensión y float32, podríamos elegir entre,
  
  
  
  • fragmentando, calculando la distancia en 64 bits y concatenando
  
  
  • recurrir a cdist en los casos en que la precisión es un problema (cómo es una pregunta abierta; por ejemplo, comunicarse con scipy podría ser útil https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-438522881 )
  
  

Luego están todos los problemas de inconsistencias entre euclidianos, sqeuclidianos, minkowski, etc.

En cuanto a las precisiones, @jeremiedbb , @amueller y yo tuvimos una charla rápida, en su mayoría solo ordeñando a Jeremie por su experiencia. Él opina que no debemos preocuparnos tanto por los problemas de inestabilidad en un contexto de ML en dimensiones altas en float64. Jeremie también dio a entender que es difícil encontrar una prueba eficiente para determinar si se han obtenido buenos resultados (cf. # 12142).

Así que creo que estamos contentos con @rth 's anterior comentario con el upcasting para float32. Dado que cdist también hace upcast a float64, podríamos reimplementar cdist para tomar float32 (¿pero con acumuladores float64?), O podríamos usar fragmentación, si queremos menos copias en float32 con poca intensidad.

¿ @Celelibi quiere cambiar el PR en # 11271, o debería alguien más (¿uno de nosotros?) Producir una solicitud de extracción completa?

Y una vez que esto se haya solucionado, creo que deberíamos hacer que sqeuclidean y minkowski (p en {0,1}) usen nuestras implementaciones. No hemos discutido la discrepancia con los vecinos más cercanos. Otro sprint :)

Después de una breve discusión en el sprint, terminamos de la siguiente manera:

• en caso de alta dimensión (> 32 o> 64 elija el mejor): upcast por fragmentos a float64 cuando es float32 y mantener el método 'rápido'. Para este tipo de datos, los problemas numéricos, en float64, son casi insignificantes (proporcionaré puntos de referencia para eso)

• en caso de baja dimensión: implemente el cálculo seguro (en lugar de usar scipy cdist debido al upcast) en sklearn.

(También es tentador lanzar upcasting float32 en 0.20.3)

Aquí hay algunos puntos de referencia para la comparación de velocidades entre scipy y sklearn.
[... recortar ...]

Esto es muy interesante. En realidad, no esperaba este resultado. Hice de nuevo su punto de referencia y encontré un resultado muy similar. Excepto que yo abogaría por un límite de decisión más bajo. Mi punto de referencia sugeriría 8 características.

El costo de equivocarse no es simétrico. cdist es mejor solo para cálculos que duran menos de unos pocos segundos y se ralentiza muy rápido cuando aumenta el número de funciones. Entonces, mejor use la implementación BLAS en caso de duda.

Editar: este punto de referencia fue para float64, pero también encuentro que la conversión ascendente de matrices float32 a float64 apenas agrega un pequeño porcentaje al tiempo total y no cambia la conclusión.

Noté que el umbral depende de la máquina en la que está ejecutando los puntos de referencia. Sospecho que puede tener que ver con las instrucciones de AVX. Me di cuenta de que los puntos de referencia que publiqué se ejecutaron en una máquina que no tenía instrucciones AVX2, solo AVX. Y en una máquina que tiene AVX2, obtuve resultados similares a los suyos.

Pero la pregunta no es solo sobre el rendimiento, sino también sobre la precisión y es más probable que tenga problemas de precisión cuando la dimensión es pequeña. Quizás 16 sea un buen compromiso. Qué piensas ?

Con respecto a esta discusión, diría que necesitamos comparar la precisión para tomar una decisión informada.

Sin embargo, en lo que respecta a sus relaciones públicas, la precisión ya no debería ser un problema. Pero a costa de un cálculo un poco más caro. Por lo tanto, el umbral probablemente debería decidirse comparando su RP.

La precisión de la evaluación comparativa no es tan fácil. Porque los casos difíciles no se distribuirán uniformemente.
Y puede ser problemático si ocurre sin ser detectado en un estuche de esquina. Por lo general, querrá tener una precisión numérica garantizada dentro de límites de CPU asequibles.
Pero como se mencionó en otra parte, una sola característica con 10000000.01 y 10000000.00 debería ser suficiente para desencadenar inestabilidad numérica con fp64 cuando se usa la ecuación problemática conocida, 10000 y 10001 con fp32. Con 1024 funciones, prueba

>>> import sklearn.metrics.pairwise as sk, scipy.spatial.distance as sp
>>> X = [[10000.01] * 1024, [10000.00] * 1024]
>>> print(sk.euclidean_distances(X,X), "\n", sp.cdist(X,X))
[[ 0.          0.31895195]
 [ 0.31895195  0.        ]] 
 [[ 0.    0.32]
 [ 0.32  0.  ]]

(esto estaba usando 0.19.1) La distancia correcta es 0.32.

Como puede ver, las inestabilidades numéricas tienden a empeorar con la cantidad de funciones (a menos que sus datos sean escasos). Aquí, el resultado tiene menos de dos dígitos de precisión con FP64.

13410 no soluciona este caso específico. es decir, float64 + alta dimensión.

Sin embargo, lo corrige para float32.

Pero decidimos que para float64 + high dim, lo mantenemos como estaba, porque es muy poco probable que ocurran problemas de precisión y no se aplican realmente a los casos de uso de aprendizaje automático.

En su ejemplo, X [0] y X [1] tienen normas iguales a 320000,32 y 320000 y su distancia es 0,32, es decir, 1e-6 veces su norma. En el aprendizaje automático, los 16 dígitos significativos (en float64) no son todos relevantes.

Pero decidimos que para float64 + high dim, lo mantenemos como estaba, porque es muy poco probable que ocurran problemas de precisión y no se aplican realmente a los casos de uso de aprendizaje automático.

Sería más moderado en este. Reducir la dimensionalidad es un primer paso habitual en ML. MDS se puede utilizar para eso, y hace un uso intensivo de la matriz de distancia euclidiana.

Si alguien quiere ver cómo mejorar la precisión del caso float64, hay una forma de usar dos flotantes para representar los resultados intermedios. Aunque creo que comienza a caer más allá del alcance de scikit-learn.
ftp://ftp.math.ethz.ch/users/wpp/CELL/qd.pdf

No estaba claro. No estoy diciendo que los datos de alta dimensión no se apliquen al aprendizaje automático. Estoy diciendo que el tipo de problemas de precisión que ocurren en float64 involucran puntos cuya distancia es 6 órdenes de magnitud más pequeña que sus normas. Tener tal precisión no tiene sentido en un modelo de aprendizaje automático realista

En el aprendizaje automático, los 16 dígitos significativos (en float64) no son todos relevantes.

No estoy del todo convencido de que esto sea así en general.

En este ejemplo, hemos perdido 15 de 16 dígitos en precisión. Estoy de acuerdo si usamos la mitad de la precisión, pero no tenemos tal relación. La pérdida de downcasting FP64 a FP32 a menudo puede ser tolerable debido a la precisión de la medición. Y las GPU de nivel de consumidor son mucho más rápidas con FP32 que con FP64, por ejemplo (aunque en algunos casos, ahora permiten datos FP32 y acumuladores FP64), y para la inferencia de redes neuronales, es posible que incluso vea int8 ahora. Pero eso no se mantiene en todas partes.

Por ejemplo, en la agrupación de k-medias, existe la suposición de que los grupos difieren sustancialmente en sus medios (y que no sabemos los medios de antemano), y por lo tanto tenemos una pérdida de precisión aquí. Si tiene muchos clústeres, algunas de sus normas pueden ser grandes en comparación con su separación.
Además, después de las primeras iteraciones iniciales, son a menudo pequeñas diferencias de distancia las que hacen que un punto cambie a otro grupo. La pérdida de precisión aquí puede afectar los resultados y podría causar inestabilidad.
Ahora considere k-medias en fragmentos de series de tiempo con muchas variables.

Con el aumento de los tamaños de los datos, debemos asumir que las distancias al vecino más cercano se hacen más pequeñas y, a menos que sus normas sean 0, eventualmente serán más pequeñas que las normas vectoriales y causarán problemas. Por lo tanto, es probable que esto se vuelva más grave al aumentar el tamaño de los conjuntos de datos. La maldición de la dimensionalidad dice que las distancias más grandes y más pequeñas se vuelven cada vez más similares; por lo que para calcular la clasificación correcta del vecino más cercano, es posible que necesitemos una buena precisión en datos de alta dimensión. En el conjunto de datos de 20news, la distancia más pequeña distinta de cero es alrededor de 0.02 (las normas son todas 1). Pero eso son solo 10k instancias y contenidos bastante diversos. Ahora suponga que el conjunto de datos se trataba de una detección casi duplicada en su lugar ...

No estaría seguro de que esto "improbable" suceda en ML ... por supuesto que no afectará a todo el mundo.

Cuando digo "En el aprendizaje automático, los 16 dígitos significativos (en float64) no son todos relevantes", no estoy hablando de la distancia calculada, estoy hablando de los datos X.
En el aprendizaje automático, sus datos provienen de una medida y no hay una medida precisa hasta el noveno dígito (además de muy pocas en física de partículas).
Entonces, en su ejemplo de 10000000.01 y 10000000.00 , ¿cómo le daría alguna importancia a una distancia de 0.01 cuando su incertidumbre sobre los valores de X es mucho mayor?

Para KMeans, primero hay una manera de superar una gran parte de las pérdidas de precisión. Cuando busca el centro más cercano de una observación x, no necesita agregar la norma de x al cálculo de la distancia, lo que evita la cancelación catastrófica en la mayoría de los casos.
Entonces, k significa grupos basados ​​en distancias euclidianas. Pero no sabe si esta es la forma exacta en que se recopilan sus datos. De hecho, existe una probabilidad 0 de que sus datos se agrupen de esa manera. Kmeans ofrece una estimación de cómo se podrían agrupar sus datos y los puntos que se encuentran en la frontera de 2 grupos definitivamente no pueden considerarse pertenecientes con certeza a uno u otro. ¿Cuál es su interpretación de un punto a la misma distancia de 2 grupos? El mío es que los 2 clústeres deben ser solo un clúster o KMeans no es el mejor algoritmo para agrupar mis datos (o incluso kmeans me da una idea bastante buena de cómo se agrupan mis datos, pero sé que las fronteras de los clústeres no son relevantes).

El uso de solo "| b | ^ 2-2ab" no tiene una cancelación catastrófica, pero la misma pérdida de precisión en los dígitos que marcan la diferencia. Los resultados son los mismos que si añadieras la norma de a a cada distancia después; si las distancias son mucho más pequeñas que la norma de a, entonces se obtiene una pérdida de precisión que se puede evitar haciendo los cálculos de la forma tradicional sin hacks BLAS.
¡Así que en realidad NO puede superar el problema numérico de esta manera!

K-means es un problema de optimización. Por lo tanto, estos trucos pueden significar que sklearn solo encuentre soluciones peores que otras herramientas. Y como se indicó anteriormente, esto también puede provocar inestabilidades. En el peor de los casos, esto podría hacer que sklearn kmeans recorra los mismos estados hasta max_iter sin mejora (asumiendo tol = 0, si desea encontrar un óptimo local), lo que la teoría diría que es imposible.
Hasta que k-means haya convergido, no se puede decir mucho sobre puntos con la "misma" distancia a dos grupos. En la siguiente iteración, los medios pueden haberse movido y la diferencia podría volverse mucho mayor e importante.
No soy un gran admirador de k-means porque no funciona demasiado bien con datos ruidosos. Pero hay variaciones que manejan mejor estos casos. Sin embargo, si lo usa, probablemente debería intentar obtener la calidad completa (por eso también uso siempre tol=0 ) y no empeorarlo de lo necesario. Es lo suficientemente barato para hacer los cálculos adecuados (y, como se mencionó, los problemas empeoran con el tamaño de los datos; por lo tanto, para datos pequeños, el tiempo de ejecución más lento generalmente no importa, para conjuntos de datos más grandes, la precisión se vuelve más importante).

Dependiendo de la aplicación, la diferencia entre 10000000.01 y 10000000.00 puede ser importante. Y como mostré antes, si usa múltiples funciones, los problemas surgen antes. Con fp32 tan solo 10000 y 10001 con una sola función y 100 frente a 101 con 100 funciones, supongo:

Como se mencionó, la media puede tener un significado físico que no querrás perder. Si tiene datos con temperaturas en Kelvin, no querrá escalarlos o centrarlos 0: 1; eso arruinaría su escala de razones . Ahora, si desea comparar, por ejemplo, series de tiempo de la temperatura de algún producto de acero a medida que se enfría, y averiguar si el proceso de enfriamiento afecta la confiabilidad de su producto de acero. Es posible que tenga temperaturas de más de 700 K, y la serie temporal puede tener cientos de puntos de datos si desea analizar el proceso de enfriamiento. Incluso con solo 5 dígitos de precisión de entrada (0.01K) con la longitud de la serie de tiempo, el problema numérico puede ocurrir. De nuevo, puede terminar con solo 1-2 dígitos en el resultado. No creo que pueda simplemente descartar que la precisión sea importante en ML si tiene este tipo de efecto catastrófico. Es diferente si pudiera garantizar obtener siempre, digamos, 10 de 16 dígitos en precisión. Aquí no puede hacer eso, puede tener 0 dígitos en el peor de los casos (por eso es catastrófico).

En el aprendizaje automático, sus datos provienen de una medida y no hay una medida precisa hasta el noveno dígito (además de muy pocas en física de partículas).

Los valores brutos del mundo real rara vez tienen ese tipo de precisión, eso es correcto. Pero ML no se limita a ese tipo de información. Uno podría querer aplicar ML a problemas matemáticos, como aplicar MDS en el gráfico de un rompecabezas en forma de cubo de Rubik o agrupar las estrategias exitosas encontradas por su enjambre de agentes de RL que juegan pacman.
Incluso si la fuente inicial de información es el mundo real, puede haber algún procesamiento intermedio que haga que la mayoría de los dígitos sean relevantes para el algoritmo de agrupamiento. Como el resultado de un descenso de gradiente en una función cuyos parámetros se muestrean estadísticamente en el mundo real.

De hecho, me pregunto por qué todavía estamos discutiendo esto. Supongo que todos estamos de acuerdo en que scikit-learn debería hacer todo lo posible en el equilibrio entre precisión y tiempo de cálculo. Y quien no esté satisfecho con el estado actual debe enviar una solicitud de extracción.

El uso de solo "| b | ^ 2-2ab" no tiene una cancelación catastrófica, pero la misma pérdida de precisión en los dígitos que marcan la diferencia. Los resultados son los mismos que si añadieras la norma de a a cada distancia después; si las distancias son mucho más pequeñas que la norma de a, entonces se obtiene una pérdida de precisión que se puede evitar haciendo los cálculos de la forma tradicional sin hacks BLAS.
¡Así que en realidad NO puede superar el problema numérico de esta manera!

Hay una pérdida de precisión, pero no puede causar una cancelación catastrófica (al menos cuando ayb están cerca), y puede mostrar que el error relativo en la distancia (que no es una distancia) permanece pequeño.
En el caso de KMeans, donde solo está interesado en encontrar el centro más cercano, tiene la precisión suficiente para mantener el orden correcto. Si al final desea la inercia, puede calcular las distancias de cada punto a su centro de grupo con la fórmula exacta.

Además, KMeans no es un problema de optimización convexa, por lo que incluso si lo deja correr con tol = 0 hasta la convergencia, termina en un mínimo local que puede estar muy lejos de los mínimos globales (incluso con la inicialización de kmeans ++). Así que prefiero ejecutar kmeans muchas veces con diferentes inicios y un número razonablemente pequeño de iteraciones. Tendrás más posibilidades de terminar en mejores mínimos locales. Luego puede volver a ejecutar el mejor hasta la convergencia.

El error relativo en comparación con la distancia real puede ser arbitrariamente grande y, por lo tanto, causar vecinos más cercanos incorrectos. Considere el caso donde | a | ² = | b | ² = 1, por ejemplo en tf-idf. Suponga que los vectores están muy cerca. Entonces ab también está cerca de 1, y en este punto ya perdió gran parte de su precisión.
Como escribí anteriormente, el error está ahí, incluso si no tiene una cancelación catastrófica. Considere 8 dígitos de precisión. La distancia real puede ser 0.000012345678 y se puede calcular con ocho dígitos usando FP32 y una distancia euclidiana regular. Pero con esta ecuación, calcula el valor ab = 0.99998765432 en su lugar, que con FP32 se truncará a aproximadamente 0.99998765 en el mejor de los casos, por lo que perdió tres dígitos de precisión innecesariamente en este ejemplo. La pérdida es tan grande como en el caso catastrófico. Si las distancias son mucho más pequeñas que las normas, su precisión puede volverse arbitrariamente mala con este enfoque.

Sí, kmeans no es convexo. Pero entonces querrá al menos encontrar un óptimo local y no quedarse atascado (o incluso oscilar porque los errores resultantes se comportan de manera errática) porque su precisión es demasiado baja. Entonces, al menos, tiene la oportunidad de encontrar el global en casos con buen comportamiento y con múltiples intentos.

Aprecio esta discusión, pero lo que realmente necesitamos es una solución que no sea peor que la que estábamos haciendo antes de que dejáramos de hacer upcasting a float64. En ese sentido, la solución upcasting @Celelibi 's fue suficiente. Usar la solución exacta en dimensiones reducidas es una mejora adicional de lo que solíamos hacer.

Con respecto a una versión futura, ¿siente más confianza para detectar de manera eficiente cuándo podríamos considerar el cálculo exacto en altas dimensiones?

Ejecuté un punto de referencia para evaluar la precisión promedio del caso float64 con números aleatorios. Comparo 3 algoritmos: neumaier_sum((x-y)**2) , numpy.sum((x-y)**2) y X2 - 2*X.dot(Y.T) + Y2.T . El resultado exacto para comparar se ha obtenido utilizando mpmath con una precisión de 256 bits.
X y Y tienen 100 muestras y un número variable de características y están llenos de números aleatorios entre -2 y 2.

En el siguiente gif, hay una imagen por número de función (entre 1 y 200). En cada imagen, cada punto representa el error relativo de la distancia euclidiana al cuadrado entre uno de los 10000 pares de vectores de X y Y . El error relativo se multiplica por 2 ^ 53 para facilitar la lectura, que corresponde aproximadamente a la unidad ULP.
Las curvas anteriores son la distribución aproximada (utilizando una estimación de densidad de grano).

Tenga en cuenta que los gráficos se cortaron a 6 ULP para facilitar la lectura. Muestra el caso promedio, no el peor de los casos. El error de la fórmula expandida puede crecer bastante.

Mi análisis de este resultado es que, en promedio, el error relativo de la fórmula expandida puede ser muy grande con pocas características, pero rápidamente se vuelve similar al de la diferencia y suma numerosa. El umbral se encuentra entre 5 y 10 características.

Actualmente también estoy tratando de encontrar un límite superior para el error de la fórmula expandida, así como ejemplos patológicos.

Creo que la preocupación de @ kno10 es que a menudo nos interesan los casos en los que
los puntos no se distribuyen aleatoriamente, sino que están cerca unos de otros o tienen unidades
norma.

En efecto, pero que necesitaba para convencerse de que, en la práctica, no es BS completa. ^^

Para completar el comentario anterior: el error relativo de la fórmula x²+y²-2ab parece no tener límites. A menos que mi análisis sea incorrecto, cuando x y y están cerca uno del otro, el error relativo puede ser de hasta 2^(52*2) . Al menos teóricamente. En la práctica, el peor de los casos que encontré es un error relativo de 2^52+1 .

>>> a, b = (0xfffffec4d6282+1) * 2.0**(511-52), 0xfffffec4d6282 * 2.0**(511-52)
>>> a, b
(6.703903473040778e+153, 6.7039034730407766e+153)
>>> exactdiff = (a-b)**2
>>> exactdiff
2.2158278651204453e+276
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> computeddiff
-9.9792015476736e+291
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0
>>> bin(int(abs((computeddiff - exactdiff) / exactdiff)))
'0b10000000000000000000000000000000000000000000000000001'

Cambiar el signo del resultado lo acercaría más a la verdad. Este es el ejemplo más dramático que pude encontrar, pero en realidad cambiar el exponente en los valores de a y b no cambia el error relativo.

>>> a, b = (0xfffffec4d6282+1) * 2.0**(-52), 0xfffffec4d6282 * 2.0**(-52)
>>> a, b
(0.9999999266202912, 0.999999926620291)
>>> exactdiff = (a-b)**2
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0

Creo que un diagrama de histograma en ULP tendría más sentido que la animación anterior con la distribución de errores dentro de ULP. Por tanto, 0 error ULP y 1 error ULP son "tan buenos como es posible". 2 Es probable que el ULP sea inevitable debido al sqrt. Supongo que vale la pena investigar cualquier error mayor.

El uso de (computed - exact) / exact es razonable siempre que el valor exacto sea grande. Pero una vez que tenemos desafíos numéricos para el valor exacto, esto se vuelve bastante inestable. En tales casos, puede valer la pena usar (computed-exact)/norm su lugar, es decir, mirando la precisión de nuestros cálculos de distancia en comparación con los datos de entrada, no en comparación con las distancias derivadas.
Si tenemos dos valores unidimensionales que solo difieren en 1 ULP y un error de 2 ULP puede parecer enorme; pero ya estamos en la resolución de datos de entrada, por lo que los resultados son bastante inestables.
Tenga en cuenta que con múltiples dimensiones, podemos obtener una resolución más alta en los datos de entrada.

Considere los datos de entrada del tipo (1, 1e-16) frente a (1, 2e-16) . Por ejemplo, si tenemos un atributo constante en los datos de entrada, digamos, un píxel blanco en MNIST.
Con la ecuación basada en diferencias esto estará bien, pero la versión de puntos se mete en problemas, ¿no es así? Es por eso que los experimentos unidimensionales pueden no ser suficientes para estudiar esto.

Creo que un diagrama de histograma en ULP tendría más sentido que la animación anterior con la distribución de errores dentro de ULP.

No estoy seguro de ver cómo lo habrías representado. Habría un histograma por número de característica y por algoritmo. No hay mucho que pueda hacer además de una trama en 3D o una animación.

El uso de (computed - exact) / exact es razonable siempre que el valor exacto sea grande. Pero una vez que tenemos desafíos numéricos para el valor exacto, esto se vuelve bastante inestable.

No estoy seguro de lo que quiere decir con inestable en este contexto. El valor exacto debe calcularse con lo que sea necesario para hacerlo exacto.
(Hablando de eso, debería haber calculado el error relativo con precisión arbitraria también en mi gráfico, en lugar de compararlo con el resultado exactamente redondeado. Actualicé mi gráfico, las ondas extrañas desaparecieron).

En tales casos, puede valer la pena usar (computed-exact)/norm su lugar, es decir, mirando la precisión de nuestros cálculos de distancia en comparación con los datos de entrada, no en comparación con las distancias derivadas.

Si entiendo su idea correctamente, preferiría comparar el error absoluto con la magnitud de los datos de entrada. Utilizar las normas vectoriales como medida agregada de la magnitud de las entradas. Mientras que el error relativo estándar lo compara con la magnitud del resultado exacto.

Creo que con esta métrica intentas capturar qué tan defectuoso es un algoritmo. Pero en realidad no parece particularmente útil por algunas razones.

• Realmente no dice cuántos dígitos del resultado son inexactos.
• En realidad, la mayoría de los algoritmos tendrían una puntuación inferior a 1e-15. Incluso la fórmula expandida (algoritmo basado en puntos) tendría una puntuación limitada por algo como 5 ULP (entrada) (estimación aproximada, no escribí la prueba completa).
• Y dado que ambas métricas son solo una versión reescalada del error absoluto computed - exact , clasificarían los algoritmos en el mismo orden cuando se evaluaran en las mismas entradas.
  Entonces, es lo mismo que el error relativo habitual, solo que con una interpretación de valor menos útil (IMO).

Considere los datos de entrada del tipo (1, 1e-16) frente a (1, 2e-16) . Por ejemplo, si tenemos un atributo constante en los datos de entrada, digamos, un píxel blanco en MNIST.
Con la ecuación basada en diferencias esto estará bien, pero la versión de puntos se mete en problemas, ¿no es así? Es por eso que los experimentos unidimensionales pueden no ser suficientes para estudiar esto.

El algoritmo basado en puntos tendría un error relativo de 1 , lo que significa que el error es tan grande como el resultado exacto y, por lo tanto, ningún dígito del resultado es correcto. Y su métrica tendría un valor de 1e-16 lo que significa que, en relación con la escala de la norma vectorial, solo el dígito 16 está desactivado.
No estoy seguro de lo que intenta mostrar con este ejemplo.

Si todavía nos preocupa la precisión de las distancias_euclidianas con float64, probablemente sea mejor resumir esta discusión en un nuevo número, ya que aquí hay 100 comentarios.